Контрольная работа: Методы и модели в экономике

, .

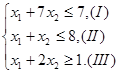
Построим на плоскости прямые ограничений, вычислив координаты точек пересечения этих прямых с осями координат (рис.2).

x 2 16 5

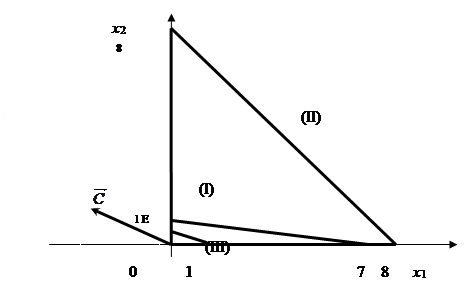
Рис.2. Графическое решение задачи при z = 3x₁ – 2x₂ → min

Строим вектор из точки (0;0) в точку (-3; 2). Точка Е (0;1) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора . Поэтому Е – это точка минимума целевой функции. Тогда минимальное значение функции равно:

.

Ответ: а) Функция z = 3x₁ – 2x₂ → max и равна 21 в точке (7;0).

б) Функция z = 3x₁ – 2x₂ → min и равна - 2 в точке (0;1).

Задача №3

Решить методом потенциалов транспортную задачу, где – цена перевозки единицы груза из пункта в пункт .

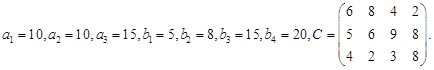
Решение

Поскольку суммарные запасы = 35 (ед. груза) и суммарные потребности = 48 (ед. груза) не совпадают (т.е. мы имеем дело с открытой транспортной задачей), необходимо ввести фиктивный пункт производства . Тогда транспортная матрица будет иметь следующий вид (табл.1).

Таблица 1- Общий вид транспортной матрицы

Пунктыпроизводства, i	Пункты потребления, j				Объем производства
	1	2	3	4
1	6	8	4	2	10
2	5	6	9	8	10
3	4	2	3	8	15
4	0	0	0	0	13
Объем потребления (спрос)	5	8	15	20	48

Найдем опорный план транспортной задачи методом северо-западного угла (табл. 2).

Таблица 2 – Транспортная матрица с опорным планом северо-западного угла

Пункты производства, i	Пункты потребления, j				Объем производства
	1	2	3	4
1	6 5	8 5	4 -	2 -	10/5/0
2	5 « 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 684 Бесплатно скачать Контрольная работа: Методы и модели в экономике >>> Скачать <<< Меню Поиск