Контрольная работа: Методы построения функции принадлежности требований к заданному уровню качества

(4)

где b - расстояние между точками перехода для μk(х), т.е. точками, в которых функция вида принимает значение 0,5.

Таким образом, задача построения μk(х) для некоторого числа сводиться к отысканию параметров а и в, чтобы можно было определить β (х), с помощью β(х) – α θ, используя α, построить μk(х).

4. Параметрический подход к построению функций принадлежности

Описываемый метод построения функций принадлежности основан на предположении, что эксперт характеризуя лингвистическое значение какого-либо признака, с минимальным напряжением может указать три точки шкалы: А, В, С, из которых В и С – точки, по его мнению, еще (или уже) не принадлежащие описываемому лингвистическому значению, А – точка, определенно принадлежащая ему.

Пусть имеются параметрическое описание термов t и tI двух значений некоторой лингвистической переменной. Один из термов может представлять собой модификацию (ограничение) другого: tI = h (t), где h – ограничение на t типа ДОВОЛЬНО, БОЛЕЕ – МЕНЕЕ, НЕ ОЧЕНЬ и т.п. Задача состоит в том, чтобы используя параметры термов t: (z1, z2, z3) и tI: (ω1, ω2, ω3) описать переход от t к tI (параметры считаются упорядоченными отношением "меньше").

Очевидно, что S – образную функцию можно рассматривать, как вырожденный случай треугольной функции, в которой один из параметров z1 или z2 стремится к бесконечности. Таким образом, задача состоит в том, чтобы описать переход между любыми двумя формами

Для решения этой задачи используется аппарат автоморфных функций. Рассмотрим дробно-линейное отображение прямой на себя вида

(5)

преобразование Т-1, обратное Т, получается, если уравнение

разрешить относительно ω:

(6)

Таким образом, при параметрическом представлении функций принадлежности задача описания перехода от одного терма t: (z1, z2, z3) к другому tI: (ω1, ω2, ω3) решается непосредственным подсчетом четырех параметров – коэффициентов дробно-линейного преобразования по формулам:

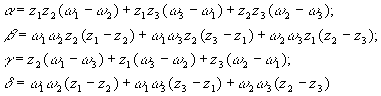(7)

Эти же коэффициенты при подстановке в (6) определяют обратный переход от tI к t.

Рассмотрим теперь переход от терма t треугольной формы к терму tI с S – образной функцией принадлежности. Для дробно-линейных преобразований этому случаю соответствует переход от одной из крайних заданных точек в положение бесконечно-удаленной точки.

Если z1 = ∞, то параметры дробно-линейного преобразования

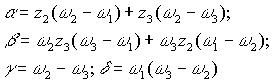(8)

Если z3 = ∞ , то

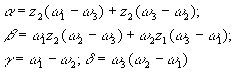(9)

Рассмотрим случай, когда функции принадлежности представляются S – образной или просто наклонной кривой. В этом случае имеет место линейное отображение прямой

(10)

Параметры преобразования (10)

(11)

Обратный переход (у → х) осуществляется по формуле

(12)

5. Построение функции принадлежности на основе ранговых оценок

Данный метод разработан А.П. Ротштейном и базируется на идее распределения степени принадлежности элементов универсального множества согласно с их рангами.