Контрольная работа: Методы построения функции принадлежности требований к заданному уровню качества

Введем также обозначения:

Тогда правило распределения степеней принадлежности можно задать в виде соотношения:

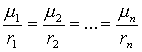(13)

к которому добавляется условие нормирования

(14)

Используя соотношение (13) легко определить степени принадлежности всех элементов универсального множества через степени принадлежности опорного элемента.

Если опорным элементом является элемент х1 Î Х с принадлежностью m 1, то

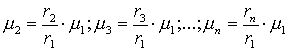(15)

Для опорного элемента х2 Î Х с принадлежностью m 2, получаем

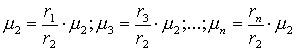(16)

Для опорного элемента хn Î Х с принадлежностью m n, имеем

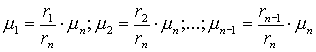(17)

Учитывая условие нормировки (14) из соотношений (15) – (17) находим:

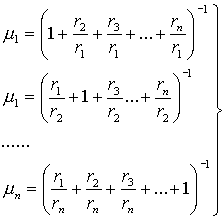(18)

Полученные формулы (18) дают возможность вычислять степени принадлежности m S(xi) двумя независимыми путями:

- по абсолютным оценкам уровней ri , , которые определяются по 9-ти бальной шкале (1 – наименьший ранг, 9 – наибольший ранг).

- по относительным оценкам рангов

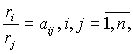
которые образуют матрицу:

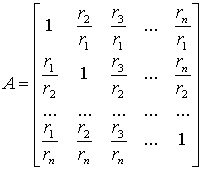(19)

Эта матрица обладает следующими свойствами:

а) она диагональная, т.е. аiі=1 ;

б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: аij=1/аji;

в) она транзитивна, т.е. аiк× акi, поскольку

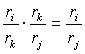
Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы А легко определить элементы всех других строк. Если известна r-я строка, т.е. элементы акj, k , , то произвольный элемент аij находиться так

Поскольку матрица (19) может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9 – ти бальную шкалу Саати: . Эта шкала приведена ранее, в табл. 1.

Таким образом, с помощью полученных формул (6.5.18), экспертные значения о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма.