Контрольная работа: Моделирование хозяйственной деятельности предприятия

КОНТРОЛЬНАЯ РАБОТА

По дисциплине

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Вариант № 6

Выполнил: Алепов А.В.

студ. 3ФК курса,

г. Южно-Сахалинск 2006 г.

№6

Привести систему к системе с базисом, найти соответствующее базисное решение и сделать проверку, подставив решение в исходную систему:

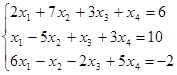
Решение:

Составим таблицу:

2	7	3	1	6
1	-5	1	3	10
6	-1	-2	5	-2
1	-5	1	3	10
2	7	3	1	6
6	-1	-2	5	-2
1	-5	1	3	10
0	17	1	-5	-14
0	29	-8	-13	-62
1	1	-5	3	10
0	1	17	-5	-14
0	-8	29	-13	-62
1	0	-22	8	24
0	1	17	-5	-14
0	0	165	-53	-174
1	0	0
0	1	0
0	0	1

Получили систему с базисом:

Здесь , , - базисные неизвестные, - свободное неизвестное. Положим . Получим , , .

Подставим решение в исходную систему:

,

решение найдено верно.

№26

Предположим, что для производства двух видов продукции А и В можно использовать только материал трех сортов. При этом на изготовление единицы изделия А расходуется 2 кг материала, 3 кг материала второго сорта, 4 кг материла третьего сорта. На изготовление единицы изделия В расходуется 5 кг материала, 2 кг материала второго сорта, 3 кг материла третьего сорта. На складе фабрики имеется всего материала первого сорта 45 кг, второго сорта - 27 кг, третьего сорта – 38 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 7 тыс. рублей, а от продукции вида В прибыль составляет 5 тыс. рублей.

Определить максимальную прибыль от реализации всей продукции видов А и В. Решить задачу симплексным методом и графически.

Решение:

1. Решение с помощью симплексного метода.

Составим математическую модель задачи. Обозначим через х₁ и х₂ выпуск продукции А и В соответственно. Затраты материала первого сорта на план составят 2х₁ + 5х₂ и они недолжны превосходить запасов 45 кг:

Аналогично, ограничения по материалу второго сорта

И по материалу третьего сорта:

Прибыль от реализации х₁ изделий А и х₂ изделий В составит

целевая функция задачи.

Получили модель задачи:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--