Контрольная работа: Моделирование хозяйственной деятельности предприятия

Решить транспортную задачу.

Решение:

1. Занесем данные задачи в таблицу:

В1	В2	В3	В4	В5
А1	5	8	7	10	3	100
А2	4	2	2	5	6	200
А3	7	3	5	9	2	200
А4	5	7	4	2	5	100
	190	100	130	80	100	600

2. Составляем математическую модель задачи: для этого вводим неизвестные х_ij , которыми являются количество единиц товара, перевозимого от каждого поставщика к каждому потребителю.

ограничения по поставкам

ограничение по потребителям

(,( ограничения по здравому смыслу.

Цель задачи (стоимость всей перевозки) в математической форме:

Задача разрешима, т.к.

.

3. Находим оптимальный план по методу наименьшего элемента

В1	В2	В3	В4	В5
А1	5100	87	76	108	33	100
А2	4-2 +	270-	2130	53	65	200
А3	- 770	+330	52	95	2100	200
А4	520	76	43	280	55	100
	190	100	130	80	100	600

- план невырожденный

Дадим оценку полученному плану методом потенциалов. Каждому поставщику А_i ставим в соответствие число (, называемое потенциалом поставщика; каждому потребителю B_j – число (, называемое потенциалом потребителя. Причем и выбираем так, чтобы в любой загруженной клетке сумма их равнялась тарифу этой клетки, т.е.

Всего занятых клеток m+ n– 1 = 8 (план не вырожденный). Придаем одному из неизвестных значение 0.

Для определения потенциалов составляем систему:

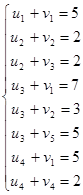
Откуда

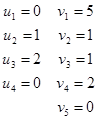
Вычисляем оценки для свободных клеток по формуле

и запишем их в левом углу свободных клеток. В клетке (2; 1) получили отрицательную оценку. Строим для нее цикл

вдоль которого перемещаем

.