Контрольная работа: Надежность информационных систем
В момент времени t + Δ t система будет находиться в состоянии kc вероятностью
(31)
– вероятность того, что система не уйдет из состояния k.
Устремив 
получим общее выражение для дифференциального уравнения
(32)
При k=0 
(33)
k=1 
(34)
k=m+1 
(35)
Начальные условия
(36)
т.е. в начальный момент времени все элементы исправны.
Уравнение (32) – уравнение А.Н. Колмогорова для однородного марковского процесса (λ = const).
Уравнению (32) можно сопоставить граф переходов из одного состояния системы в другое
На основании анализа уравнений А.Н. Колмогорова, Б.В. Васильева [1] было сформулировано мнемоническое правило составления таких уравнений по заданному графу. В левой части каждого уравнения стоит производная по времени от вероятности нахождения системы в k-м состоянии в момент времени t. Число членов в правой части равно алгебраической сумме произведений интенсивностей переходов на соответствующие вероятности пребывания системы в тех узлах графа, откуда совершается непосредственный переход системы в другие (соседние) узлы. Причем, слагаемым, которым соответствуют выходящие из k-го узла стрелки графа, приписывается – знак минус, а входящем – знак плюс. Как видим уравнение (32) составлено по этому правилу.
Применяя преобразование Лапласа:
(37)
систему дифференциальных уравнений сводим к алгебраической, решая которую получим
(38)
Зная изображение 
по Лапласу находим
(39)
Решая (39), получим
, (40)
где 
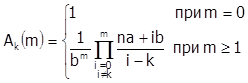(41)
Окончательно
, (42)
где 
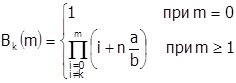(43)
Например, m=1, a/b=1
B0 (1)=1+n; B1 (1)=n
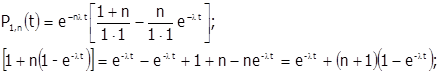(44)
(45)
