Контрольная работа: Обусловленность матрицы

Норма матрицы A: =57,3638

Норма обратной матрицы : =129841,19

7448184,055

Теоретическая оценка погрешности

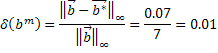
Так как то матрица плохо обусловлена, это значит, что незначительные изменения в правой части приведут к большой погрешности в решении.

Задача 2 Метод хорд

Методом хорд найти корень уравнения с точностью .

Решение

Найдем интервал, в котором находится корень:

Корнем уравнения является точка пересечения этих функций

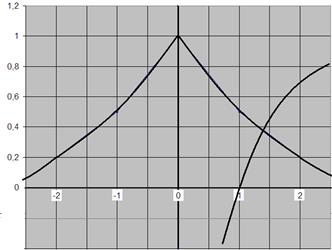
Из графика видно, что корень лежит в интервале .

Найдем неподвижный конец:

Для определения используем horda.xls(см. приложение)

y(a)	-0,5	y(b)	0,493147	непод
y'(a)	1,5	y'(b)	0,66	1
y''(a)	-1,75	y''(b)	-0,426

Неподвижный конец -1

Выполняем приближение, используя horda.xls

Х	х0
1	2
xi	F(xi)	sigma
1,50345005	0,1010481	else
1,41881012	0,0179259	else
1,40431471	0,0030870	else
1,40183381	0,0005288	else
1,40140927	0,0000905	else
1,40133662	0,0000155	else
1,40132419	0,0000027	and

Окончание процесса – при ,это и есть наш корень.

Задача 3 Решение СЛАУ

Решить систему уравнений ax=b, где

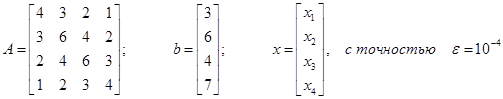
Вычислить точностные оценки методов по координатам: , - координаты численного решения, - координаты точного решения.

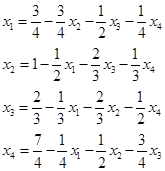
1. Метод простых итераций