Контрольная работа: Обусловленность матрицы
Решение, наиболее близкое к точному, получено из таблицы 3
Х1=1,4740
Х2=1,9479
Х3=0,9109
Х4=2,9879
Найдём![]() :
:
| xi | xi* | |xi-xi*| |
| 0 | 1,474 | 1,474 |
| 1 | 1,9479 | 0,9479 |
| -1 | 0,9109 | 1,9109 |
| 2 | 2,9879 | 0,9879 |
| max | 1,9109 |
![]() (МПИ)=1,9109
(МПИ)=1,9109
2. Метод Зейделя
Сделаем расчет, используя SLAU.xls
| х1 | 0,7500 | 0,0000 | 0,0000 | 0,0000 | 0,7500 | 0,0000 | |
| х2 | 1,0000 | -0,3750 | 0,0000 | 0,0000 | 0,6250 | 0,0000 | 1 |
| х3 | 0,6667 | -0,2500 | 0,0000 | 0,0000 | 0,4167 | 0,0000 | |
| х4 | 1,7500 | -0,1875 | -0,3125 | -0,3125 | 0,9375 | 0,0000 |
| х1 | 0,7500 | -0,4688 | -0,2084 | -0,2344 | -0,1615 | 0,7500 | |
| х2 | 1,0000 | 0,0807 | -0,2778 | -0,3125 | 0,4904 | 0,6250 | 2 |
| х3 | 0,6667 | 0,0538 | -0,4167 | -0,4688 | -0,1649 | 0,4167 | |
| х4 | 1,7500 | 0,0404 | -0,2452 | 0,1237 | 1,6688 | 0,9375 |
| х1 | 0,7500 | -0,7499 | 0,5000 | -0,5000 | 0,0000 | 0,0000 | |
| х2 | 1,0000 | 0,0000 | 0,6666 | -0,6667 | 0,9999 | 0,9999 | 30 |
| х3 | 0,6667 | 0,0000 | -0,6666 | -1,0000 | -0,9999 | -0,9999 | |
| х4 | 1,7500 | 0,0000 | -0,5000 | 0,7500 | 2,0000 | 2,0000 |
Решение, наиболее близкое к точному, получено на 30 шаге вычислений
Х1=0
Х2=0,9999
Х3=0,9999
Х4=2
Найдём![]() :
:
| xi | xi* | |xi-xi*| |
| 0 | 0,0000 | 0,0000 |
| 1 | 0,9999 | -0,0001 |
| -1 | -0,9999 | 0,0001 |
| 2 | 2,0000 | 0,0000 |
| max | 0,0001 |
![]() =0,0001
=0,0001
Вывод: МПИ - быстрее сходится, но обладает меньшей точностью, чем метод Зейделя, который дольше сходится.
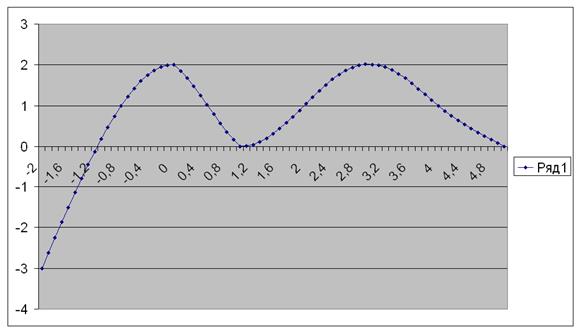
Задача 4 Сплайн интерполяция
| Х | У |
| -2,00 | -3,00 |
| 0,00 | 2,00 |
| 1,00 | 0,00 |
| 3,00 | 2,00 |
| 4,00 | 1,00 |
| 5,00 | 0,00 |
Для вычислений используем splain.xls
Найдем ![]() :
:
| hi=xi - xi-1 | |
| h0 | 2,00 |
| h1 | 1,00 |
| h2 | 2,00 |
| h3 | 1,00 |
| h4 | 1,00 |
Для вычисления q будем использовать метод прогонки.
Вычислим массивы коэффициентов a,b,c и правой части d:
| a | b | c | d | |
| 0 | 0,0000 | 1,0000 | 0,1667 | -4,50 |
| 1 | 0,1667 | 1,0000 | 0,3333 | 3,00 |
| 2 | 0,3333 | 1,0000 | 0,1667 | -2,00 |
| 3 | 0,1667 | 0,6667 | 0,0000 | 0,00 |
Вычисление прогоночных коэффициентов:
| A[ ] | B[ ] |
| 0,00 | 0,00 |
| -0,16667 | -4,5 |
| -0,34286 | 3,857143 |
| -0,18817 | -3,70968 |
| 0 | 0,973202 |
Теперь вычисляем ![]()
| x | y |
| -2 | -3 |
| -1,9 | -2,62093 |
| -1,8 | -2,24381 |
| -1,7 | -1,87056 |
| -1,6 | -1,50314 |
| -1,5 | -1,14348 |
| -1,4 | -0,79353 |
| -1,3 | -0,45522 |
| -1,2 | -0,13049 |
| -1,1 | 0,178702 |
| -1 | 0,47043 |
| -0,9 | 0,74275 |
| -0,8 | 0,99372 |
| -0,7 | 1,221401 |
| -0,6 | 1,423849 |
| -0,5 | 1,599126 |
| -0,4 | 1,74529 |
| -0,3 | 1,860401 |
| -0,2 | 1,942516 |
| -0,1 | 1,989696 |
| 0 | 2 |
| 0,1 | 1,852492 |
| 0,2 | 1,673571 |
| 0,3 | 1,470644 |
| 0,4 | 1,251116 |
| 0,5 | 1,02239 |
| 0,6 | 0,791874 |
| 0,7 | 0,566972 |
| 0,8 | 0,355088 |
| 0,9 | 0,163629 |
| 1 | 0 |
| 1,1 | 0,005772 |
| 1,2 | 0,043163 |
| 1,3 | 0,108555 |
| 1,4 | 0,198332 |
| 1,5 | 0,308877 |
| 1,6 | 0,436575 |
| 1,7 | 0,577807 |
| 1,8 | 0,728958 |
| 1,9 | 0,886412 |
| 2 | 1,046551 |
| 2,1 | 1,205759 |
| 2,2 | 1,360419 |
| 2,3 | 1,506916 |
| 2,4 | 1,641631 |
| 2,5 | 1,760949 |
| 2,6 | 1,861253 |
| 2,7 | 1,938927 |
| 2,8 | 1,990354 |
| 2,9 | 2,011917 |
| 3 | 2 |
| 3,1 | 1,989668 |
| 3,2 | 1,946922 |
| 3,3 | 1,876445 |
| 3,4 | 1,78292 |
| 3,5 | 1,67103 |
| 3,6 | 1,545457 |
| 3,7 | 1,410885 |
| 3,8 | 1,271996 |
| 3,9 | 1,133473 |
| 4 | 1 |
| 4,1 | 0,872264 |
| 4,2 | 0,753286 |
| 4,3 | 0,642094 |
| 4,4 | 0,537715 |
| 4,5 | 0,439175 |
| 4,6 | 0,345501 |
| 4,7 | 0,255719 |
| 4,8 | 0,168858 |
| 4,9 | 0,083942 |
| 5 | 0 |
Задача 5 Решение дифференциального уравнения
![]()
Для расчета использован файл diffur.xls
Мы выбираем шаг h, рассчитываем значения для точки х+2h с шагом h и 2h, если проверка на окончание процесса показала < δ, то берем шаг h и считаем с ним остальные точки, если же нет – берем новое h и снова делаем проверку
| {1,2} | x | y | k1 | 0,00004000 | k2 | 0,00004000 | k3 | 0,00004000 | k4 | 0,00004000 |
| y(1)=1 | 1 | 1 | ||||||||
| 1,00001 | 1,00002 | ∆y | 0,00004000 | y1 | 1,00004000 | |||||
| 1,00001 | 1,00002 | |||||||||
| 1,00002 | 1,00004 | |||||||||
| 0,00002 | ||||||||||
| x | y | k1 | 0,00004018 | k2 | 0,00004018 | k3 | 0,00004018 | k4 | 0,00004018 | |
| 1,1 | 1,00004 | |||||||||
| 1,10001 | 1,00006 | ∆y | 0,00004018 | y2 | 1,00008018 | |||||
| 1,10001 | 1,00006 | |||||||||
| 1,10002 | 1,00008 | |||||||||
| 0,00002 | ||||||||||
| x | y | k1 | 0,00004066 | k2 | 0,00004066 | k3 | 0,00004066 | k4 | 0,00004066 | |
| 1,2 | 1,00008 | |||||||||
| 1,20001 | 1,000101 | ∆y | 0,00004066 | y2 | 1,00012084 | |||||
| 1,20001 | 1,000101 | |||||||||
| 1,20002 | 1,000121 |
| {1,2} | x | y | k1 | 0,000080000 | k2 | 0,000079997 | k3 | 0,000079997 | k4 | 0,000079994 |
| y(1)=1 | 1 | 1 | ||||||||
| 1,00002 | 1,00004 | ∆y | 0,000079997 | y1 | 1,000079997 | |||||
| 1,00002 | 1,00004 | |||||||||
| 1,00004 | 1,00008 | |||||||||
| 0,00004 | ||||||||||
| x | y | k1 | 0,000081327 | k2 | 0,000081324 | k3 | 0,000081324 | k4 | 0,000081321 | |
| 1,2 | 1,00008 | |||||||||
| 1,20002 | 1,000121 | ∆y | 0,000081324 | y2 | 1,000161321 | |||||
| 1,20002 | 1,000121 | |||||||||
| 1,20004 | 1,000161 | |||||||||
| 0,00004 | ||||||||||
| x | y | k1 | 0,000084558 | k2 | 0,000084555 | k3 | 0,000084555 | k4 | 0,000084551 | |
| 1,4 | 1,000161 | |||||||||
| 1,40002 | 1,000204 | ∆y | 0,000084555 | y2 | 1,000245875 | |||||
| 1,40002 | 1,000204 | |||||||||
| 1,40004 | 1,000246 |
R=0,000008 <0,00001Процесс закончен – шаг = 0,00004 Для наглядности возьмем шаг = 0,01
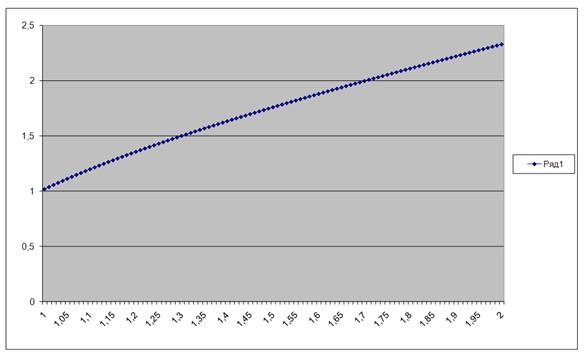
| xk1 | xk2 | xk3 | xk4 | y | k1 | yk2 | k2 | yk3 | k3 | yk4 | k4 | ∆y | y |
| 1 | 1,005 | 1,005 | 1,01 | 1 | 0,02 | 1,01 | 0,019802 | 1,009901 | 0,019804 | 1,019804 | 0,019613 | 0,019804 | 1,019804 |
| 1,01 | 1,015 | 1,015 | 1,02 | 1,019804 | 0,019613 | 1,029611 | 0,019427 | 1,029518 | 0,019429 | 1,039233 | 0,019249 | 0,019429 | 1,039233 |
| 1,02 | 1,025 | 1,025 | 1,03 | 1,039233 | 0,019249 | 1,048857 | 0,019074 | 1,04877 | 0,019076 | 1,058309 | 0,018906 | 0,019076 | 1,058309 |
| 1,03 | 1,035 | 1,035 | 1,04 | 1,058309 | 0,018906 | 1,067762 | 0,018742 | 1,06768 | 0,018743 | 1,077052 | 0,018583 | 0,018743 | 1,077052 |
| 1,04 | 1,045 | 1,045 | 1,05 | 1,077052 | 0,018583 | 1,086344 | 0,018428 | 1,086266 | 0,01843 | 1,095482 | 0,018279 | 0,01843 | 1,095482 |
| 1,05 | 1,055 | 1,055 | 1,06 | 1,095482 | 0,018279 | 1,104621 | 0,018132 | 1,104548 | 0,018133 | 1,113615 | 0,01799 | 0,018133 | 1,113615 |
| 1,06 | 1,065 | 1,065 | 1,07 | 1,113615 | 0,01799 | 1,12261 | 0,017851 | 1,12254 | 0,017852 | 1,131467 | 0,017717 | 0,017852 | 1,131467 |
| 1,07 | 1,075 | 1,075 | 1,08 | 1,131467 | 0,017717 | 1,140325 | 0,017585 | 1,140259 | 0,017586 | 1,149053 | 0,017457 | 0,017586 | 1,149053 |
| 1,08 | 1,085 | 1,085 | 1,09 | 1,149053 | 0,017457 | 1,157781 | 0,017332 | 1,157719 | 0,017333 | 1,166386 | 0,017211 | 0,017333 | 1,166386 |
| 1,09 | 1,095 | 1,095 | 1,1 | 1,166386 | 0,017211 | 1,174991 | 0,017092 | 1,174931 | 0,017092 | 1,183478 | 0,016976 | 0,017092 | 1,183478 |
| 1,1 | 1,105 | 1,105 | 1,11 | 1,183478 | 0,016976 | 1,191966 | 0,016863 | 1,191909 | 0,016864 | 1,200342 | 0,016753 | 0,016864 | 1,200342 |
| 1,11 | 1,115 | 1,115 | 1,12 | 1,200342 | 0,016753 | 1,208718 | 0,016645 | 1,208664 | 0,016645 | 1,216987 | 0,01654 | 0,016645 | 1,216987 |
| 1,12 | 1,125 | 1,125 | 1,13 | 1,216987 | 0,01654 | 1,225257 | 0,016436 | 1,225205 | 0,016437 | 1,233424 | 0,016336 | 0,016437 | 1,233424 |
| 1,13 | 1,135 | 1,135 | 1,14 | 1,233424 | 0,016336 | 1,241592 | 0,016238 | 1,241543 | 0,016238 | 1,249663 | 0,016142 | 0,016238 | 1,249663 |
| 1,14 | 1,145 | 1,145 | 1,15 | 1,249663 | 0,016142 | 1,257734 | 0,016048 | 1,257686 | 0,016048 | 1,265711 | 0,015956 | 0,016048 | 1,265711 |
| 1,15 | 1,155 | 1,155 | 1,16 | 1,265711 | 0,015956 | 1,273689 | 0,015866 | 1,273644 | 0,015866 | 1,281577 | 0,015778 | 0,015866 | 1,281577 |
| 1,16 | 1,165 | 1,165 | 1,17 | 1,281577 | 0,015778 | 1,289466 | 0,015692 | 1,289423 | 0,015692 | 1,297269 | 0,015607 | 0,015692 | 1,297269 |
| 1,17 | 1,175 | 1,175 | 1,18 | 1,297269 | 0,015607 | 1,305073 | 0,015525 | 1,305032 | 0,015525 | 1,312794 | 0,015444 | 0,015525 | 1,312794 |
| 1,18 | 1,185 | 1,185 | 1,19 | 1,312794 | 0,015444 | 1,320516 | 0,015364 | 1,320476 | 0,015365 | 1,328159 | 0,015287 | 0,015365 | 1,328159 |
| 1,19 | 1,195 | 1,195 | 1,2 | 1,328159 | 0,015287 | 1,335803 | 0,01521 | 1,335764 | 0,015211 | 1,34337 | 0,015136 | 0,015211 | 1,34337 |
| 1,2 | 1,205 | 1,205 | 1,21 | 1,34337 | 0,015136 | 1,350938 | 0,015063 | 1,350901 | 0,015063 | 1,358433 | 0,014991 | 0,015063 | 1,358433 |
| 1,21 | 1,215 | 1,215 | 1,22 | 1,358433 | 0,014991 | 1,365929 | 0,014921 | 1,365893 | 0,014921 | 1,373354 | 0,014852 | 0,014921 | 1,373354 |
| 1,22 | 1,225 | 1,225 | 1,23 | 1,373354 | 0,014852 | 1,38078 | 0,014784 | 1,380746 | 0,014784 | 1,388138 | 0,014718 | 0,014784 | 1,388138 |
| 1,23 | 1,235 | 1,235 | 1,24 | 1,388138 | 0,014718 | 1,395497 | 0,014652 | 1,395465 | 0,014653 | 1,402791 | 0,014588 | 0,014653 | 1,402791 |
| 1,24 | 1,245 | 1,245 | 1,25 | 1,402791 | 0,014588 | 1,410085 | 0,014525 | 1,410054 | 0,014526 | 1,417317 | 0,014464 | 0,014526 | 1,417317 |
| 1,25 | 1,255 | 1,255 | 1,26 | 1,417317 | 0,014464 | 1,424549 | 0,014403 | 1,424518 | 0,014404 | 1,43172 | 0,014344 | 0,014404 | 1,43172 |
| 1,26 | 1,265 | 1,265 | 1,27 | 1,43172 | 0,014344 | 1,438892 | 0,014285 | 1,438863 | 0,014286 | 1,446006 | 0,014228 | 0,014286 | 1,446006 |
| 1,27 | 1,275 | 1,275 | 1,28 | 1,446006 | 0,014228 | 1,45312 | 0,014172 | 1,453092 | 0,014172 | 1,460178 | 0,014116 | 0,014172 | 1,460178 |
| 1,28 | 1,285 | 1,285 | 1,29 | 1,460178 | 0,014116 | 1,467236 | 0,014062 | 1,467209 | 0,014062 | 1,47424 | 0,014009 | 0,014062 | 1,47424 |
| 1,29 | 1,295 | 1,295 | 1,3 | 1,47424 | 0,014009 | 1,481245 | 0,013956 | 1,481218 | 0,013956 | 1,488196 | 0,013904 | 0,013956 | 1,488196 |
| 1,3 | 1,305 | 1,305 | 1,31 | 1,488196 | 0,013904 | 1,495149 | 0,013853 | 1,495123 | 0,013854 | 1,50205 | 0,013804 | 0,013854 | 1,50205 |
| 1,31 | 1,315 | 1,315 | 1,32 | 1,50205 | 0,013804 | 1,508952 | 0,013754 | 1,508927 | 0,013755 | 1,515805 | 0,013706 | 0,013755 | 1,515805 |
| 1,32 | 1,325 | 1,325 | 1,33 | 1,515805 | 0,013706 | 1,522658 | 0,013658 | 1,522634 | 0,013659 | 1,529463 | 0,013612 | 0,013659 | 1,529463 |
| 1,33 | 1,335 | 1,335 | 1,34 | 1,529463 | 0,013612 | 1,536269 | 0,013566 | 1,536246 | 0,013566 | 1,543029 | 0,013521 | 0,013566 | 1,543029 |
| 1,34 | 1,345 | 1,345 | 1,35 | 1,543029 | 0,013521 | 1,54979 | 0,013476 | 1,549767 | 0,013476 | 1,556505 | 0,013432 | 0,013476 | 1,556505 |
| 1,35 | 1,355 | 1,355 | 1,36 | 1,556505 | 0,013432 | 1,563222 | 0,013389 | 1,5632 | 0,013389 | 1,569895 | 0,013347 | 0,013389 | 1,569895 |
| 1,36 | 1,365 | 1,365 | 1,37 | 1,569895 | 0,013347 | 1,576568 | 0,013305 | 1,576547 | 0,013305 | 1,5832 | 0,013264 | 0,013305 | 1,5832 |
| 1,37 | 1,375 | 1,375 | 1,38 | 1,5832 | 0,013264 | 1,589832 | 0,013223 | 1,589811 | 0,013223 | 1,596423 | 0,013183 | 0,013223 | 1,596423 |
| 1,38 | 1,385 | 1,385 | 1,39 | 1,596423 | 0,013183 | 1,603015 | 0,013144 | 1,602995 | 0,013144 | 1,609567 | 0,013106 | 0,013144 | 1,609567 |
| 1,39 | 1,395 | 1,395 | 1,4 | 1,609567 | 0,013106 | 1,61612 | 0,013067 | 1,616101 | 0,013068 | 1,622635 | 0,01303 | 0,013068 | 1,622635 |
| 1,4 | 1,405 | 1,405 | 1,41 | 1,622635 | 0,01303 | 1,62915 | 0,012993 | 1,629132 | 0,012993 | 1,635628 | 0,012957 | 0,012993 | 1,635628 |
| 1,41 | 1,415 | 1,415 | 1,42 | 1,635628 | 0,012957 | 1,642106 | 0,012921 | 1,642088 | 0,012921 | 1,648549 | 0,012885 | 0,012921 | 1,648549 |
| 1,42 | 1,425 | 1,425 | 1,43 | 1,648549 | 0,012885 | 1,654992 | 0,012851 | 1,654974 | 0,012851 | 1,6614 | 0,012816 | 0,012851 | 1,6614 |
| 1,43 | 1,435 | 1,435 | 1,44 | 1,6614 | 0,012816 | 1,667808 | 0,012782 | 1,667791 | 0,012783 | 1,674182 | 0,012749 | 0,012783 | 1,674182 |
| 1,44 | 1,445 | 1,445 | 1,45 | 1,674182 | 0,012749 | 1,680557 | 0,012716 | 1,68054 | 0,012716 | 1,686899 | 0,012684 | 0,012716 | 1,686899 |
| 1,45 | 1,455 | 1,455 | 1,46 | 1,686899 | 0,012684 | 1,693241 | 0,012652 | 1,693225 | 0,012652 | 1,699551 | 0,012621 | 0,012652 | 1,699551 |
| 1,46 | 1,465 | 1,465 | 1,47 | 1,699551 | 0,012621 | 1,705861 | 0,01259 | 1,705846 | 0,01259 | 1,71214 | 0,012559 | 0,01259 | 1,71214 |
| 1,47 | 1,475 | 1,475 | 1,48 | 1,71214 | 0,012559 | 1,71842 | 0,012529 | 1,718405 | 0,012529 | 1,724669 | 0,012499 | 0,012529 | 1,724669 |
| 1,48 | 1,485 | 1,485 | 1,49 | 1,724669 | 0,012499 | 1,730919 | 0,01247 | 1,730904 | 0,01247 | 1,737139 | 0,012441 | 0,01247 | 1,737139 |
| 1,49 | 1,495 | 1,495 | 1,5 | 1,737139 | 0,012441 | 1,743359 | 0,012412 | 1,743345 | 0,012412 | 1,749551 | 0,012384 | 0,012412 | 1,749551 |
| 1,5 | 1,505 | 1,505 | 1,51 | 1,749551 | 0,012384 | 1,755743 | 0,012356 | 1,75573 | 0,012356 | 1,761908 | 0,012329 | 0,012356 | 1,761908 |
| 1,51 | 1,515 | 1,515 | 1,52 | 1,761908 | 0,012329 | 1,768072 | 0,012302 | 1,768059 | 0,012302 | 1,77421 | 0,012275 | 0,012302 | 1,77421 |
| 1,52 | 1,525 | 1,525 | 1,53 | 1,77421 | 0,012275 | 1,780348 | 0,012249 | 1,780334 | 0,012249 | 1,786459 | 0,012223 | 0,012249 | 1,786459 |
| 1,53 | 1,535 | 1,535 | 1,54 | 1,786459 | 0,012223 | 1,79257 | 0,012197 | 1,792558 | 0,012197 | 1,798656 | 0,012172 | 0,012197 | 1,798656 |
| 1,54 | 1,545 | 1,545 | 1,55 | 1,798656 | 0,012172 | 1,804742 | 0,012147 | 1,80473 | 0,012147 | 1,810804 | 0,012123 | 0,012147 | 1,810804 |
| 1,55 | 1,555 | 1,555 | 1,56 | 1,810804 | 0,012123 | 1,816865 | 0,012098 | 1,816853 | 0,012098 | 1,822902 | 0,012074 | 0,012098 | 1,822902 |
| 1,56 | 1,565 | 1,565 | 1,57 | 1,822902 | 0,012074 | 1,828939 | 0,012051 | 1,828927 | 0,012051 | 1,834953 | 0,012027 | 0,012051 | 1,834953 |
| 1,57 | 1,575 | 1,575 | 1,58 | 1,834953 | 0,012027 | 1,840966 | 0,012004 | 1,840955 | 0,012004 | 1,846957 | 0,011981 | 0,012004 | 1,846957 |
| 1,58 | 1,585 | 1,585 | 1,59 | 1,846957 | 0,011981 | 1,852948 | 0,011959 | 1,852936 | 0,011959 | 1,858916 | 0,011937 | 0,011959 | 1,858916 |
| 1,59 | 1,595 | 1,595 | 1,6 | 1,858916 | 0,011937 | 1,864884 | 0,011915 | 1,864873 | 0,011915 | 1,870831 | 0,011893 | 0,011915 | 1,870831 |
| 1,6 | 1,605 | 1,605 | 1,61 | 1,870831 | 0,011893 | 1,876777 | 0,011872 | 1,876766 | 0,011872 | 1,882702 | 0,011851 | 0,011872 | 1,882702 |
| 1,61 | 1,615 | 1,615 | 1,62 | 1,882702 | 0,011851 | 1,888628 | 0,01183 | 1,888617 | 0,01183 | 1,894532 | 0,011809 | 0,01183 | 1,894532 |
| 1,62 | 1,625 | 1,625 | 1,63 | 1,894532 | 0,011809 | 1,900437 | 0,011789 | 1,900427 | 0,011789 | 1,906321 | 0,011769 | 0,011789 | 1,906321 |
| 1,63 | 1,635 | 1,635 | 1,64 | 1,906321 | 0,011769 | 1,912205 | 0,011749 | 1,912195 | 0,011749 | 1,91807 | 0,011729 | 0,011749 | 1,91807 |
| 1,64 | 1,645 | 1,645 | 1,65 | 1,91807 | 0,011729 | 1,923935 | 0,01171 | 1,923925 | 0,01171 | 1,92978 | 0,011691 | 0,01171 | 1,92978 |
| 1,65 | 1,655 | 1,655 | 1,66 | 1,92978 | 0,011691 | 1,935625 | 0,011672 | 1,935616 | 0,011672 | 1,941452 | 0,011653 | 0,011672 | 1,941452 |
| 1,66 | 1,665 | 1,665 | 1,67 | 1,941452 | 0,011653 | 1,947278 | 0,011635 | 1,947269 | 0,011635 | 1,953087 | 0,011616 | 0,011635 | 1,953087 |
| 1,67 | 1,675 | 1,675 | 1,68 | 1,953087 | 0,011616 | 1,958895 | 0,011598 | 1,958886 | 0,011599 | 1,964685 | 0,011581 | 0,011599 | 1,964685 |
| 1,68 | 1,685 | 1,685 | 1,69 | 1,964685 | 0,011581 | 1,970475 | 0,011563 | 1,970467 | 0,011563 | 1,976248 | 0,011546 | 0,011563 | 1,976248 |
| 1,69 | 1,695 | 1,695 | 1,7 | 1,976248 | 0,011546 | 1,982021 | 0,011528 | 1,982012 | 0,011529 | 1,987777 | 0,011512 | 0,011529 | 1,987777 |
| 1,7 | 1,705 | 1,705 | 1,71 | 1,987777 | 0,011512 | 1,993533 | 0,011495 | 1,993524 | 0,011495 | 1,999272 | 0,011478 | 0,011495 | 1,999272 |
| 1,71 | 1,715 | 1,715 | 1,72 | 1,999272 | 0,011478 | 2,005011 | 0,011462 | 2,005002 | 0,011462 | 2,010733 | 0,011446 | 0,011462 | 2,010733 |
| 1,72 | 1,725 | 1,725 | 1,73 | 2,010733 | 0,011446 | 2,016456 | 0,01143 | 2,016448 | 0,01143 | 2,022163 | 0,011414 | 0,01143 | 2,022163 |
| 1,73 | 1,735 | 1,735 | 1,74 | 2,022163 | 0,011414 | 2,02787 | 0,011398 | 2,027862 | 0,011398 | 2,033561 | 0,011383 | 0,011398 | 2,033561 |
| 1,74 | 1,745 | 1,745 | 1,75 | 2,033561 | 0,011383 | 2,039252 | 0,011367 | 2,039245 | 0,011367 | 2,044928 | 0,011352 | 0,011367 | 2,044928 |
| 1,75 | 1,755 | 1,755 | 1,76 | 2,044928 | 0,011352 | 2,050604 | 0,011337 | 2,050597 | 0,011337 | 2,056265 | 0,011322 | 0,011337 | 2,056265 |
| 1,76 | 1,765 | 1,765 | 1,77 | 2,056265 | 0,011322 | 2,061927 | 0,011308 | 2,061919 | 0,011308 | 2,067573 | 0,011293 | 0,011308 | 2,067573 |
| 1,77 | 1,775 | 1,775 | 1,78 | 2,067573 | 0,011293 | 2,07322 | 0,011279 | 2,073213 | 0,011279 | 2,078852 | 0,011265 | 0,011279 | 2,078852 |
| 1,78 | 1,785 | 1,785 | 1,79 | 2,078852 | 0,011265 | 2,084485 | 0,011251 | 2,084478 | 0,011251 | 2,090103 | 0,011237 | 0,011251 | 2,090103 |
| 1,79 | 1,795 | 1,795 | 1,8 | 2,090103 | 0,011237 | 2,095722 | 0,011223 | 2,095715 | 0,011223 | 2,101327 | 0,01121 | 0,011223 | 2,101327 |
| 1,8 | 1,805 | 1,805 | 1,81 | 2,101327 | 0,01121 | 2,106931 | 0,011196 | 2,106925 | 0,011196 | 2,112523 | 0,011183 | 0,011196 | 2,112523 |
| 1,81 | 1,815 | 1,815 | 1,82 | 2,112523 | 0,011183 | 2,118115 | 0,01117 | 2,118108 | 0,01117 | 2,123693 | 0,011157 | 0,01117 | 2,123693 |
| 1,82 | 1,825 | 1,825 | 1,83 | 2,123693 | 0,011157 | 2,129272 | 0,011144 | 2,129265 | 0,011144 | 2,134838 | 0,011132 | 0,011144 | 2,134838 |
| 1,83 | 1,835 | 1,835 | 1,84 | 2,134838 | 0,011132 | 2,140404 | 0,011119 | 2,140397 | 0,011119 | 2,145957 | 0,011107 | 0,011119 | 2,145957 |
| 1,84 | 1,845 | 1,845 | 1,85 | 2,145957 | 0,011107 | 2,15151 | 0,011095 | 2,151504 | 0,011095 | 2,157052 | 0,011082 | 0,011095 | 2,157052 |
| 1,85 | 1,855 | 1,855 | 1,86 | 2,157052 | 0,011082 | 2,162593 | 0,01107 | 2,162587 | 0,01107 | 2,168122 | 0,011059 | 0,01107 | 2,168122 |
| 1,86 | 1,865 | 1,865 | 1,87 | 2,168122 | 0,011059 | 2,173651 | 0,011047 | 2,173645 | 0,011047 | 2,179169 | 0,011035 | 0,011047 | 2,179169 |
| 1,87 | 1,875 | 1,875 | 1,88 | 2,179169 | 0,011035 | 2,184686 | 0,011024 | 2,184681 | 0,011024 | 2,190193 | 0,011012 | 0,011024 | 2,190193 |
| 1,88 | 1,885 | 1,885 | 1,89 | 2,190193 | 0,011012 | 2,195699 | 0,011001 | 2,195693 | 0,011001 | 2,201194 | 0,01099 | 0,011001 | 2,201194 |
| 1,89 | 1,895 | 1,895 | 1,9 | 2,201194 | 0,01099 | 2,206689 | 0,010979 | 2,206683 | 0,010979 | 2,212173 | 0,010968 | 0,010979 | 2,212173 |
| 1,9 | 1,905 | 1,905 | 1,91 | 2,212173 | 0,010968 | 2,217657 | 0,010957 | 2,217651 | 0,010957 | 2,22313 | 0,010947 | 0,010957 | 2,22313 |
| 1,91 | 1,915 | 1,915 | 1,92 | 2,22313 | 0,010947 | 2,228603 | 0,010936 | 2,228598 | 0,010936 | 2,234066 | 0,010926 | 0,010936 | 2,234066 |
| 1,92 | 1,925 | 1,925 | 1,93 | 2,234066 | 0,010926 | 2,239529 | 0,010915 | 2,239523 | 0,010915 | 2,244981 | 0,010905 | 0,010915 | 2,244981 |
| 1,93 | 1,935 | 1,935 | 1,94 | 2,244981 | 0,010905 | 2,250434 | 0,010895 | 2,250428 | 0,010895 | 2,255876 | 0,010885 | 0,010895 | 2,255876 |
| 1,94 | 1,945 | 1,945 | 1,95 | 2,255876 | 0,010885 | 2,261318 | 0,010875 | 2,261313 | 0,010875 | 2,266751 | 0,010865 | 0,010875 | 2,266751 |
| 1,95 | 1,955 | 1,955 | 1,96 | 2,266751 | 0,010865 | 2,272183 | 0,010855 | 2,272178 | 0,010855 | 2,277606 | 0,010846 | 0,010855 | 2,277606 |
| 1,96 | 1,965 | 1,965 | 1,97 | 2,277606 | 0,010846 | 2,283029 | 0,010836 | 2,283024 | 0,010836 | 2,288442 | 0,010827 | 0,010836 | 2,288442 |
| 1,97 | 1,975 | 1,975 | 1,98 | 2,288442 | 0,010827 | 2,293855 | 0,010817 | 2,293851 | 0,010817 | 2,299259 | 0,010808 | 0,010817 | 2,299259 |
| 1,98 | 1,985 | 1,985 | 1,99 | 2,299259 | 0,010808 | 2,304663 | 0,010799 | 2,304659 | 0,010799 | 2,310058 | 0,01079 | 0,010799 | 2,310058 |
| 1,99 | 1,995 | 1,995 | 2 | 2,310058 | 0,01079 | 2,315453 | 0,010781 | 2,315449 | 0,010781 | 2,320839 | 0,010772 | 0,010781 | 2,320839 |
| 2 | 2,005 | 2,005 | 2,01 | 2,320839 | 0,010772 | 2,326225 | 0,010763 | 2,326221 | 0,010763 | 2,331602 | 0,010754 | 0,010763 | 2,331602 |