Контрольная работа: Определение интегралов

Перейдем к замене переменных в определенном интеграле:

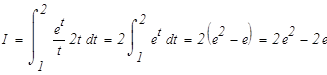
Задание. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.

Решение. Площадь области S, ограниченной снизу функцией g(x), сверху- функцией f(x), слева - вертикальной прямой , справа - вертикальной прямой равна равна определенному интегралу:

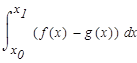
Так как мы пока не знаем, какая же из функций является большей на отрезке , построим чертеж. Точки , являются абсциссами точек пересечения графиков этих двух функций.

Как видно из построения парабола лежит выше прямой на отрезке, поэтому:

Абсциссы точек пересечения суть соответственно -6 и -1. Эти значения мы также можем получить решив в системе уравнения двух кривых

по теореме Виета имеем: , . Теперь осталось только применить формулу вычисления площади криволинейной области:

-6

-1

Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию при

Решение: имеем линейное уравнение первого порядка. будем искать решение уравнения в виде произведения двух функций от х:

Запишем исходное выражение в виде: