Контрольная работа: Определение статистических данных
Для определения средней суммы вкладов способов моментов воспользуемся формулой:
= m1 Δ*I+Ai
где: m1 – момент первого порядка
x – варианта
i – величина интервала
f – частота
Δ – постоянная величина, на которую уменьшаются все значения признака.
m1 =(Σ((X-A) / i))*f) / Σf
=(( Σ ((X-A) / i*f) / Σf)*i+A
1. Находим середины интервалов
(200 + 400) / 2 = 300 – для закрытых интервалов;
Для открытых интервалов вторая граница достраивается: (0 + 200) / 2 = 100
Величина интервала i = 200.
Наибольшая частота равна 370, следовательно А = 700.
В вариационных рядах с равными интервалами в качестве А принимается вариант с наибольшей частотой.
Число вкладчиков 
f=900
m1 = (-240-200-200+150) / 900=-0,544
=-0,544*200+700=591,2 грн.
Вывод: в среднем сумма вкладов составляет 591,2 грн.
2. Определим дисперсию способом моментов:
σ22 =i2 * (m2 -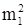 
)
m1 =-0.544; m2 =(Σ((X-A) / i)2 *f) / Σf
m2 =1470/900=1,63
σ2 =2002 *(1,63-(-0,544)2 )=53362,56 среднеквадратичное отклонение:
=231 грн.
3. Соотношение среднеквадратичного отклонения к средней называют квадратичным коэффициентом вариации:
V=(σ/)*100%=(231/591,2)*100=39,07%
4. Предельная ошибка выборки средней вычисляется по формуле:
Δx=t*
2/n
Δx=2*
(грн.)
где: n – выбранной совокупности, n=900
σ2 – дисперсия
t – коэффициент доверия (табличное значение для вероятности 0,954 соответствует t=2)