Контрольная работа: Определение статистических данных

Товарооборот в среднем возрос на 100 %.

Взаимосвязь индексов:

1,333 * 1,5 = 2,0

Задача 6

Имеются данные о выпуске одноименной продукции и её себестоимости по двум заводам

Завод	Производство продукции, тыс. шт.		Себестоимость 1 шт., грн.
	I квартал	II квартал	I квартал	II квартал
I	100	180	100	96
II	60	90	90	80

Вычислите индексы: 1) себестоимости переменного состава; 2) себестоимости постоянного состава; 3) структурных сдвигов. Поясните полученные результаты.

Решение.

Индекс себестоимости переменного состава вычисляется по формуле:

где z₀ и z₁ - себестоимость единицы продукции соответственно базисного и отчетного периодов;

q₀ и q₁ - количество (физический объем) продукции соответственно в базисном и отчетном периодах.

Индекс показывает, что средняя себестоимость по двум заводам повысилась на 71,6%, это повышение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры продукции (увеличением объема выпуска).

Выявим влияние каждого из этих факторов.

Индекс себестоимости постоянного состава вычисляется по формуле:

То есть себестоимость продукции по двум заводам в среднем возросла на 70 %.

Индекс себестоимости структурных сдвигов вычисляется по формуле:

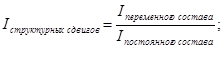
Или

Взаимосвязь индексов:

170*100,9=171,6

Вывод:

Индекс себестоимости переменного состава зависит от изменения уровня себестоимости и от изменения объема производства, т.е. средний прирост себестоимости составил 71,6 %.

Индекс себестоимости постоянного состава показывает изменение себестоимости при фиксированном объеме производства, т.е. в среднем по заводам себестоимость повысилась на 71% . Индекс себестоимости переменного состава выше, чем индекс себестоимости постоянного состава, это свидетельствует о том, что произошли благоприятные структурные сдвиги. Индекс структурных сдвигов равен 1,009 %, т.е. за счет изменения объемов производства по заводам средняя себестоимость повысилась на 0,9 %.

Задача 7

Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак Y) и оснащенностью заводов основными производственными фондами (факторный признак X) по данным задачи 1 вычислить коэффициент детерминации и эмпирическое корреляционное отношение.

Решение.

Показателем тесноты связи между факторами, является линейный коэффициент корреляции.