Контрольная работа: Определение вероятности событий
Имеем 5 черных шаров и 10 других.
Из 5 черных — 2 — ![]() событий.
событий.
Из 10 других — 1 — ![]() событий. Общее число благоприятных событий
событий. Общее число благоприятных событий
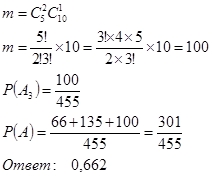
4. В ящике 5 мячей, из которых три — новые. Для игры взяли два мяча, после игры вернув их в ящик. Для второй игры случайно взяли еще два мяча. Найти вероятность того, что они оба новые
Здесь имеем два независимых события. Применяем формулу умножения вероятностей
Для того, чтобы вероятность события искомого (А) не была равна нулю в ящике после наступления события В (взяли первый раз два мяча) должно остаться либо три, либо два мяча новых.
Обозначим через В1 — взяли два мяча подержанных.
Число вариантов, что из двух мячей взяли два равно ![]() .
.
Число вариантов, что из трех мячей не взяли ни одного равно ![]()
Общее число благоприятных событий
![]() .
.
![]()
Общее количество событий — ![]() .
.

Для события А вычислим вероятность наступления при условии наступления события ![]() .
.
Имеем в ящике 5 шаров, из них три новых, тогда число благоприятных событий будет состоять из суммы:
1) Из 2-х старых мячей в выборке не оказалось ни одного — ![]() .
.
2) Из 3-х новых мячей в выборке 2 новых — ![]() .
.
Общее число благоприятных событий:
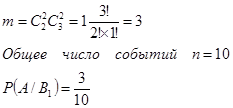
Обозначим через В 2 — (взяли первый раз один новый мяч и один старый).
Число событий — из трех мячей взяли один равно — ![]() , число вариантов — из двух мячей взяли один равно —
, число вариантов — из двух мячей взяли один равно — ![]() , общее число благоприятных вариантов равно —
, общее число благоприятных вариантов равно — ![]() .
.
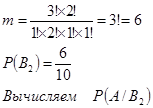
Имеем три старых и два новых мяча. Количество благоприятных событий:
— из трех старых — ни одного — ![]()
— из двух новых — два — ![]() будет равно
будет равно ![]()
Вероятность ![]() .
.
Вероятность наступления события А будет равна: