Контрольная работа: Определение вероятности событий

5. Пассажир может ждать летной погоды трое суток, после чего едет поездом. По прогнозам вероятность летной погоды в первые сутки 0,5, во вторые — 0,6, в третьи — 0,8, Х — число полных суток до отъезда пассажира.

Найти:

А) ряд распределения Х.

Вероятность того, что пассажир не будет ждать равна вероятности летней погоды в первые сутки, т.е. Р(0)=0,5.

Вероятность, что пассажир улетит через сутки равна вероятности того, что в первые сутки будет нелетная погода, а во вторые — летная, т.е.

.

Вероятность того, что пассажир улетит через двое суток равна вероятности трех независимых событий: первые сутки — нелетная погода; вторые — нелетная; третьи — летная

Вероятность того, что пассажир уедет поездом через трое суток равна вероятности того, что все трое суток погода нелетная

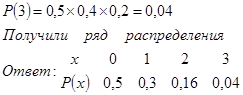
Б) функцию распределения F ( x ).

Функцию F ( x ) строим с помощью формулы:

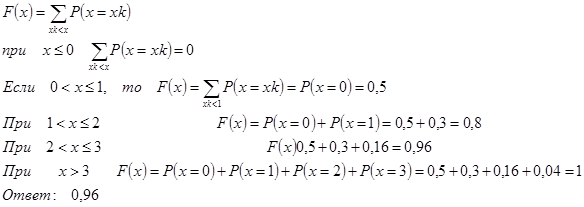
В) m _x ищем по формуле:

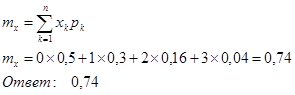
Г) D _x применяем формулу:

т.е. дисперсия равна математическому ожиданию квадрата ее отклонения:

Д) В данном промежутке x принимает только одно значение x =2, следовательно:

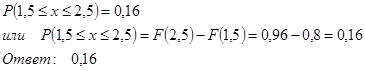
6. Дана функция распределения случайной величины

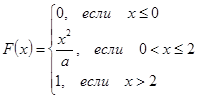
Найти:

А) константу а.

Из условия непрерывности F ( x ) следует

Б) р( x ), по определению , т.к. F ’( x ) при равно (0)’=0, при