Контрольная работа: Определители и их применение в алгебре и геометрии

Посчитаем определители обеих матриц. Получим:

det A=(-1)⁰ *((a₁₁ *a₂₂ *a₃₃ +a₁₂ *a₂₃ *a₃₁ +a₂₁ *a₃₂ *a₁₃ )-(a₁₃ *a₂₂ *a₃₁ +a₂₁ *a₁₂ *a₃₃ +a₃₂ *a₂₃ *a₁₁ ))

det B=(-1)² *((a₃₁ *a₂₂ *a₁₃ +a₂₁ *a₁₂ *a₃₃ +a₃₂ *a₂₃ *a₁₁ )-(a₃₃ *a₂₂ *a₁₁ +a₁₂ *a₂₃ *a₃₁ +a₂₁ *a₃₂ *a₁₃ ))

(a₁₁ *a₂₂ *a₃₃ +a₁₂ *a₂₃ *a₃₁ +a₂₁ *a₃₂ *a₁₃ )-(a₁₃ *a₂₂ *a₃₁ +a₂₁ *a₁₂ *a₃₃ +a₃₂ *a₂₃ *a₁₁ ) +(a₃₁ *a₂₂ *a₁₃ +a₂₁ *a₁₂ *a₃₃ +a₃₂ *a₂₃ *a₁₁ )-(a₃₃ *a₂₂ *a₁₁ +a₁₂ *a₂₃ *a₃₁ +a₂₁ *a₃₂ *a₁₃ )=0

Получили, что det A=-det B.

Свойство доказано.

Свойство №4: Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.

Доказательство:

Возьмём матрицу, в которой элементы первого столбца равны a_ij +b_j и посчитаем её определитель.

.

Раскроем скобки и приведём подобные слагаемые.

.

То есть: .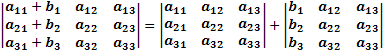

Свойство доказано.

Свойство №5: Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

Доказательство:

Пусть дан определитель detA≠0, содержащий две равные строки.

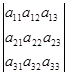= detA ; =

Поменяем местами эти равные строки. Получим новый определитель.

.

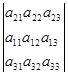Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA =0 . Свойство доказано.

Свойство №6: Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

Доказательство:

Возьмём матрицу коэффициентов и посчитаем её определитель.