Контрольная работа: Определители и их применение в алгебре и геометрии
Смешанное произведение 
по абсолютному значению равно объёму параллелепипеда, образованного векторами 
и 
знак зависит от того, является ли эта тройка векторов правой или левой.
Теорема: векторно-скалярное произведение (АВС)=(А*В)С трёх некомпланарных векторов есть число, абсолютная величина которого выражает объём параллелепипеда, построенного на векторах А, В и С, как на рёбрах. Знак произведения положителен, если векторы А, В и С образуют систему, одноимённую с основной
5. Векторное произведение векторов, заданных проекциями
Обозначим через x1 ,y1 ,z1 проекции вектора А, а через x2 ,y2 ,z2 проекции вектора В. Выразим через них векторное произведение А*В:
АxВ=(ix1 +jy1 +kz1 )*(ix2 +jy2 +kz2 ).
По распределительному свойству суммы векторов умножаются как многочлены:
АxВ=(i*i)x1 x2 +(j*i)y1 x2 +(k*i)z1 x2 +(i*j)x1 y2 +(j*j)y1 y2 +(k*j)z1 y2 +(i*k)x1 z2 +(j*k)y1 z2 +(k*k)z1 z2 . (1)
Так как I, j, k являются тремя взаимно перпендикулярными единичными векторами и вращение от j к k представляется с конца вектора i совершающимся против часовой стрелки, то:
.
Следовательно в полученном выражении (1) для АВ пропадут три слагаемых, остальные же соединятся попарно, и окончательная формула будет:
АxВ=i(y1 z2 -y2 z1 )+j(z1 x2 -z2 x1 )+k(x1 y2 -x2 y1 ).
Последнюю формулу можно также записать в символический, лёгко запоминаемой форме, если воспользоваться понятием определителя 3-го порядка.
.
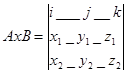Вектор 
имеет координаты 
. Вектор 
имеет координаты 
. Тогда 
Так как верна формула 
, то и следующая формула верна
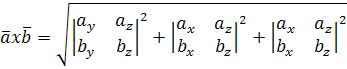
6. Примеры решение задач (с использованием определителей)
Пример 1.
Найти площадь треугольника АВС с вершинами в точках А(x1 ; y1 ; z1 ), B(x2 ; y2 ; z2 ), C(x3 ; y3 ; z3 ).
Решение:
Так как вектор 
имеет проекции x2 -x1 , y2 -y1 , z2 -z1 а вектор 
имеет проекции x3 -x1 , y3 -y1 , z3 -z1 , то площадь треугольника
=
.
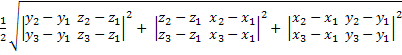Пример 2.
Определить синус угла А треугольника АВС с вершинами А(1,2,3), В(3,4,5), С(2,4,7).