Контрольная работа: Определители и их применение в алгебре и геометрии

Спроектируем вектор А= на плоскость, перпендикулярную к С⁰ , и полученную вектор-проекцию ₁ повернём в этой плоскости вокруг точки О по часовой стрелке на 90⁰ (если смотреть на плоскость с конца вектора С⁰ ).

Полученный вектор ₂ и равен А*С⁰ . В самом деле,

1) ОА₂ =ОА₁ =Аcos(90⁰ -φ)=Asinф, где ф – угол между векторами А и С⁰ ;

2) Вектор ₂ перпендикулярен к векторам А и С⁰ представляется совершающимся против часовой стрелки. Итак, ₂ =А*С⁰ .

Пусть теперь даны единичный вектор С⁰ , перпендикулярная к нему плоскость р и треугольник ОА₁ В₁ (рис. 2.), в котором ₁ =А, =В и ₁ =А+В.

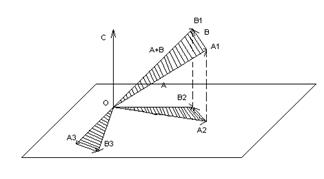
рис. 2.

Спроектируем треугольник ОА₁ В₁ на плоскость р и повернём против проекцию ОА₂ В₂ в плоскости р по часовой стрелке на 90⁰ .

Получим треугольник ОА₃ В₃ , в котором по предыдущему

₃ =(А+В)*С⁰ , ₃ =В*С⁰ , =В*С⁰ .

Так как = + , то (А+В)*С⁰ =А*С⁰ + В*С⁰ .(1)

Заметив, что С=С*С⁰ , умножим теперь обе части равенства (1) на скаляр С. Применив свойство 2 векторного произведения, получим:

(А+В)*СС

4. Справедливость этого утверждения основана на том, что площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними, что, в свою очередь, следует непосредственно из определения векторного произведения векторов А и В. (рис. 3,4)

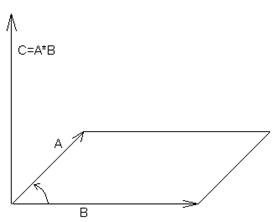
рис. 3

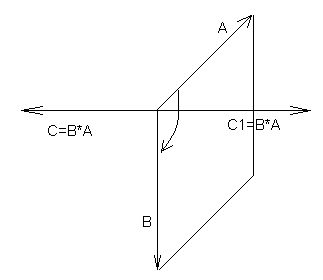
Рис. 4

4. Смешанное произведение

Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и :

.

Иногда его называют тройным скалярным произведением векторов.

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения.

Смешанное произведение в правой декартовой системе координат равно определителю матрицы, составленной из векторов и :

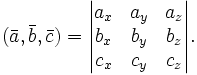
В частности,