Контрольная работа: Оптимізація економічних показників
8x1-x2-4x3≥1
-6x1-2x2+x3≤2
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
8x1-1x2-4x3-1x4 + 0x5 = 1
-6x1-2x2 + 1x3 + 0x4 + 1x5 = 2
Введемо штучні змінні х.
8x1-1x2-4x3-1x4 + 0x5 + 1x6 = 1
-6x1-2x2 + 1x3 + 0x4 + 1x5 + 0x6 = 2
Задачу на максимум цільову функцію запишемо так:
F(X) = -48x1-5x2+12x3 - Mx6 =>max
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
X1 = (0,0,0,0,2,1)
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 |
| 0 | x6 | 1 | 8 | -1 | -4 | -1 | 0 | 1 |
| x5 | 2 | -6 | -2 | 1 | 0 | 1 | 0 | |
| Індекснийрядок | F(X0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Перейдемо до основного алгоритму симплекс-метода.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 1 | x6 | 1 | 8 | -1 | -4 | -1 | 0 | 1 | 0.125 |
| x5 | 2 | -6 | -2 | 1 | 0 | 1 | 0 | 0 | |
| Індекснийрядок | F(X1) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 |
| 2 | x1 | 0.125 | 1 | -0.125 | -0.5 | -0.125 | 0 | 0.125 |
| x5 | 2.75 | 0 | -2.75 | -2 | -0.75 | 1 | 0.75 | |
| Індекснийрядок | F(X2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Оптимальний план можливо записати так:
x1 = 0.125
x5 = 2.75
F(X) = -48*0.13 = -6
Завдання 3
Розв’язати транспортну задачу.
| 1 | 4 | 7 | 8 | 1 | 200 |
| 2 | 3 | 1 | 4 | 1 | 150 |
| 5 | 1 | 3 | 2 | 3 | 350 |
| 120 | 130 | 200 | 180 | 110 |
Розв’язок
Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і-го пункту виробництва до j-го споживача 
. Оскільки 
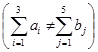, то задачу треба закрити, тобто збалансувати (зрівняти) поставки й потреби:
У нашому випадку робиться це введенням фіктивного постачальника, оскільки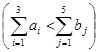 
.З уведенням фіктивного постачальника в транспортній таблиці додатково заявляється n робочих клітинок (додатковий рядок).
Виникає проблема, які ціни присвоїти цим клітинкам, щоб фіктивний рядок був нейтральним щодо оптимального вибору планових перевезень. Нейтральність забезпечується тим, що всі ціни у фіктивних клітинках вибираються однаковими, а оскільки ці ціни при поставках не повинні впливати на значення цільової функції f, то їх беруть усі рівними нулю.
Занесемо вихідні дані у таблицю.
| В1 | В2 | В3 | В4 | В5 | Запаси | |
| А1 | 1 | 4 | 7 | 8 | 1 | 200 |
| А2 | 2 | 3 | 1 | 4 | 1 | 150 |
| А3 | 5 | 1 | 3 | 2 | 3 | 350 |
| А4 | 0 | 0 | 0 | 0 | 0 | 40 |
| Потреби | 120 | 130 | 200 | 180 | 110 |
Забезпечивши закритість розв'язуваної задачі, розпочинаємо будувати математичну модель даної задачі:
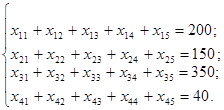
Економічний зміст записаних обмежень полягає в тому, що весь вантаж потрібно перевезти по пунктах повністю.