Контрольная работа: Оптимизация организационных решений

А₀ А₃ А₄ А₂ А₁ А₀

А₀ А₃ А₁ А₄ А₂ А₀

75 + 10 = 85

60 + 40 = 100

85 + 20 = 105

80 + 5 = 85

Таким образом, устанавливаем, что есть два равноценных оптимальных варианта последовательности строительства объектов.

Задание №4

Оптимизация очередности строительства объектов

в неритмичных потоках

Определить оптимальную очередность строительства нескольких объектов, при которой достигается минимальная общая продолжительность строительства, а также величину общей продолжительности строительства при исходной и оптимальной очередности строительства объектов.

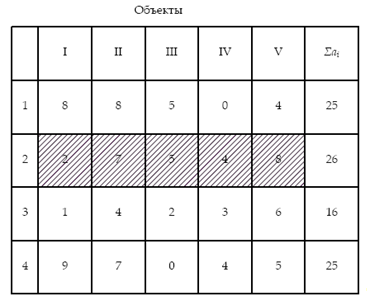
Выделяем поток №3 как поток наибольшей продолжительности. Затем по каждому объекту находим общее рабочее время, предшествующее потоку наибольшей продолжительности и общее рабочее время, последующее за потоком наибольшей продолжительности.

В третью строку под матрицей записываем со своим знаком разницу между продолжительностью работы на данном объекте последней и первой бригад.

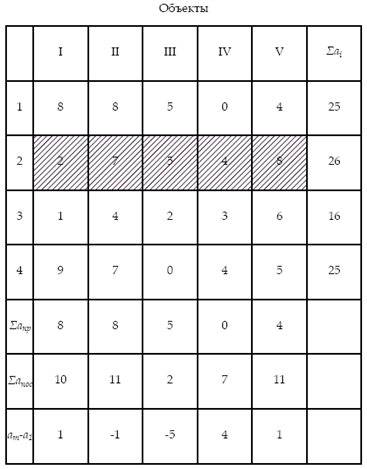
На основе данных дополнительных строк устанавливается рациональная очередность строительства объектов из следующих соображений:

а) на первом месте располагается объект с наибольшим значением Σа_пос . Остальные объекты располагаются так, чтобы Σа_пр постепенно возрастало, а Σа_пос снижалась к концу матрицы;

б) на первом месте располагается объект с наибольшим значением (а _m - а₁ ) , на последнем – с минимальным значением (а _m - а₁ ) ; остальные объекты располагаются так, чтобы (а _m - а₁ ) изменялось постепенно от максимального значения к минимальному.

Принятая очередность строительства объектов по п. а :

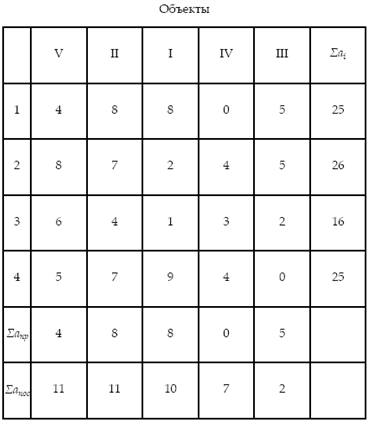
Принятая очередность строительства объектов по п. б :

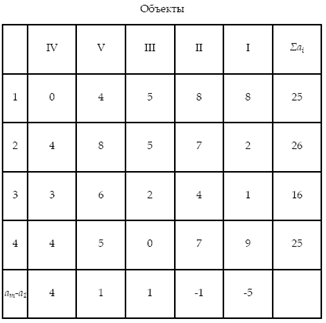
Найдем общую продолжительность строительства комплекса:

а) при исходной очередности объектов

Т₁ = (8 + 8 + 5 + 0 + 4) + (6 + 5 + 4) + (5 + 4) = 49;

б) при очередности объектов 5-2-1-4-3

Т₂ = (4 + 8 + 8 + 0 + 5) + (5 + 2 + 0) + (2 + 0) = 34;

в) при очередности объектов 4-5-3-2-1

Т₃ = (0 + 4 + 5 + 8 + 8) + (2 + 1 + 9) + (1 + 9) = 47.