Контрольная работа: Основные понятия алгебры множеств
bÎA
переводится с символического языка как "bявляется элементом множества A" или "элемент b принадлежит множеству A". Если известны все элементы множества (например, a, b и c), то общепринятой является такая запись множества:
A={a,b,c}.
В этом случае элементы множества принято заключать в фигурные скобки. Кроме того, при перечислении элементов порядок несущественен, т.е. A={a,b,c}={c,b,a}={a,c,b} и т.д.
Множества могут быть заданы двумя способами: с помощью формулировки характерных признаков (например, множество K цифр, обозначающих четные числа) или с помощью перечисления элементов (например, K = {0, 2, 4, 6, 8})
В современной математике пока что нет четкого определения отношения принадлежности. В алгебре множеств этой неопределенности можно избежать, если считать, что это отношение связывает два разных типа объектов ("элемент"Î"множество"), но ни в коем случае не должно быть связи типа "множество"Î"множество".
Между множествами устанавливается другое вроде бы похожее, но в то же время принципиально отличающееся отношение – включение, структурные свойства которого в современной математике определены достаточно четко и однозначно. Рассмотрим его более подробно. Допускаются два отличающихся варианта этого отношения:
"Ì" – строго включено;
"Í" – включено или равно.
Запись AÌB означает, что множество A включено в множество B, т.е. все элементы множества A являются одновременно элементами множества B, но при этом невозможно равенство этих множеств. Запись AÍB означает, что множество A включено в множество B, но при этом не исключается, что они могут быть равными. Изображение отношения включения с помощью кругов Эйлера показано на рисунке 2. В данном случае не обязательно использовать правильные круги. Для изображения множества может подойти любая замкнутая фигура.
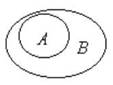
Рис. 2
Если множества заданы с помощью перечисления элементов, то отношение включения (или невключения) одного множества в другое множество можно легко установить, если сравнить элементы этих множеств. Например, если заданы множества
P ={a, b, c, d, e}; Q ={b, d, a}; R ={a, c, f},
то можно легко установить, что QÌP, но в то же время отношение RÌP для этих множеств неверно, так как элемент f из множества R не является элементом множества P.
Порядок перечисления элементов для множеств несущественен. Например, множества {b,d,a}; {a, b, d}; {d, a, b} – это по сути одно и то же множество. Если же порядок перечисления множеств является существенным, то в этом случае имеем дело не с множествами, а с последовательностями или с упорядоченными множествами (некоторые сведения о них приведены ниже). Математические свойства последовательностей существенно отличаются от математических свойств множеств.
Заметим, что несходство отношений принадлежности и включения можно иллюстрировать следующим примером. Допустим, aÎP, из чего следует, что a является элементом, а P – множеством. Можно ли в этом случае записать aÍP? Оказывается, нельзя, потому что отношение включения применимо только для двух множеств. Правильной в этом случае является запись {a}ÍP, в которой слева записан не элемент, а одноэлементное множество.
Рассмотрим еще одно отношение между множествами – отношение равенства. Множества равны, если у них одни и те же элементы. Для доказательства равенства двух множеств, особенно в тех случаях, когда у них большое или бесконечное число элементов, используется следующее определение.
Определение 1. Множества A и B равны, если справедливо как AÍB, так и BÍA.
Если множества связаны отношениями AÌB или AÍB, то в этом случае множество A называют подмножеством множества B. Среди всех возможных подмножеств произвольного множества A обязательно содержится также и само множество A. Другими словами, для любого множества A всегда справедливо AÍA.
В алгебре множеств особо выделяется и часто используется множество, которое называется "пустое множество" (обозначается "Æ"). Интуитивно пустое множество означает множество, не содержащее никаких элементов. Но это интуитивное определение не раскрывает полностью его сути и роли в алгебре множеств. В большей степени его суть раскрывается в следующем предложении, которое можно отнести к одной из аксиом алгебры множеств:
Пустое множество включено в любое множество.
Для пояснения смысла этого предложения рассмотрим следующий пример. Пусть A – множество крокодилов. Ясно, что это множество может иметь какие-то подмножества. Например, множество C крокодилов, живущих в зоопарках. Тогда отношение между A и C можно записать как CÌA. Рассмотрим еще одно подмножество множества A: подмножество крокодилов, говорящих на русском языке. Ясно, что это пустое множество и, тем не менее, можем его считать подмножеством множества A. В математических рассуждениях, когда нам надо доказать, что данное множество X не существует (или существует), сводим доказательство существования к доказательству отношения X=Æ (или X¹Æ). Часто такой метод позволяет намного упростить доказательство.
Если множество задано перечислением элементов, то часто интерес представляет совокупность всех подмножеств этого множества. Например, для множества A={a, b, c} такая совокупность состоит из восьми подмножеств:
Æ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}.
Само множество А является подмножеством самого себя. Известно также простое соотношение, позволяющее сразу же узнать общее число всех возможных подмножеств множества, содержащего ровно N элементов. Оказывается, что для любого N такое число равно 2N . Например, для нашего множества A={a, b, c} число всех возможных подмножеств равно 23 .
Обычно во многих рассуждениях используется некоторый набор множеств. Такой набор называется в алгебре множеств системой множеств. В систему множеств при этом помимо пустого множества включается и универсум, т.е. множество, для которого все множества системы множеств являются подмножествами. Другими словами, системой множеств является некоторая совокупность подмножеств некоторого множества, принятого за универсум. Например, для множеств планет, комет, звезд и т.д. в качестве универсума можно принять множество астрономических объектов.
Для универсума нет общепринятых обозначений. Далее будем обозначать его символом U.
Перейдем к операциям. Начнем с операции дополнения, которая может быть определена только тогда, когда для системы множеств задан универсум.