Контрольная работа: Основные понятия алгебры множеств
Следующие законы алгебры множеств связывают друг с другом отношения включения и равенства:
10. Из AÍB следует:
10a. AÇB = A;
10b. AÈB = B;
10c. ![]() ÈB = U;
ÈB = U;
10d. AÇ![]() = Æ.
= Æ.
Соотношение 10d можно выразить также с помощью операции разности множеств:
10e. Из AÍB следует A\B = Æ.
Следующие законы в логике и алгебре множеств называются законами де Моргана:
11a. ![]() =
=![]() È
È![]() ;
;
11b ![]() =
=![]() Ç
Ç![]() .
.
И, наконец, приведем два закона, которые определяют основные свойства отношения включения. Их используют в дальнейшем в правилах логического вывода.
12a. Если AÍB и BÍC, то AÍC (закон транзитивности включения);
12b. Если AÍB, то справедливо также и ![]() Í
Í![]() (закон контрапозиции).
(закон контрапозиции).
В математической литературе приводятся разные способы обоснования этих законов. Многие из них весьма сложны для понимания. Здесь рассмотрим относительно простой способ, который называется комбинаторным.
Пусть нам необходимо вывести некоторые законы для двух множеств X и Y. Рассмотрим диаграмму Эйлера (рисунок 7), на которой изображены эти множества и объемлющий их универсум (U).
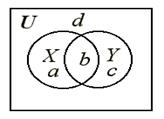
Рис. 7
Выделим на диаграмме участки a, b, c и d, которые не имеют внутренних границ, т.е. выполним разбиение нашего универсума на непересекающиеся друг с другом множества. Такое разбиение позволяет нам представить эти множества как элементы, из которых состоят универсум U и множества X и Y. Тогда для них справедливы соотношения:
U = {a, b, c, d}; X = {a, b}; Y = {b, c}.
Примем эти соотношения в качестве исходных данных и докажем для этого общего представления данной системы из двух множеств один из законов де Моргана ![]() =
=![]() È
È![]() . Тогда получим:
. Тогда получим:
1) XÇY = {b};
2) ![]() = {a, c, d};
= {a, c, d};
3) ![]() = {c, d};
= {c, d};
4) ![]() = {a, d};
= {a, d};
5) ![]() È
È![]() ={a, c, d};
={a, c, d};
6) сравнивая 2 и 5 заключаем, что ![]() =
=![]() È
È![]() , что и требовалось доказать.
, что и требовалось доказать.
Закон транзитивности (12a) интуитивно понятен. Рассмотрим обоснование закона контрапозиции (12b). Поскольку он действителен только в том случае, когда XÍY, то придется немного изменить нашу исходную систему. Для этого примем, что множество, представленное в системе элементом a, равно пустому множеству, и поэтому его можно исключить из универсума. Тогда получим следующие исходные данные:
U = {b, c, d}; X = {b}; Y = {b, c}.