Контрольная работа: Основные понятия алгебры множеств

В логике дополнению множества соответствует связка "не". Например "не красный" – любой возможный цвет кроме красного. Обычно дополнение множества обозначается с помощью черты, расположенной над символьным обозначением этого множества. Например, является обозначением дополнения множества .

Пример 1. Пусть U={a, b, c, d} и P={a, c}. Тогда ={b, d}.

Определим еще две основные операции – пересечение и объединение множеств.

Определение 3. Пересечением множеств A и B называется множество C, все элементы которого являются одновременно элементами множеств A и B.

Операция пересечения множеств обозначается символом "Ç". Символически определение 3 можно записать как формулу

C = AÇB.

Например, пересечением множества всех студентов данного вуза и множества всех участников КВН, является множество студентов данного вуза, участвующих в КВН. Другой пример: пересечением множества всех чисел, делящихся на 2, и множества всех чисел, делящихся на 3, является множество всех чисел, делящихся на 6.

В логике операции пересечения соответствует логическая связка "И" (обозначается как Ù или &). Если речь идет об объектах со свойствами P или Q, то логическая формула PÙQ означает, что речь идет только об объектах, которым присущи оба этих свойства. Если, допустим, свойствам P и Q соответствуют некоторые множества S_P и S_Q , то пересечение этих множеств S_P ÇS_Q , будет состоять из элементов, каждому из которых одновременно присущи свойства P и Q

Пример 2. Пусть A={a, b, c, d} и P={a, c, f}. Тогда AÇP = {a, c}.

Определение 4. Объединением множеств A и B называется множество C, все элементы которого являются элементами по крайней мере одного из этих множеств.

Операция объединения множеств обозначается символом "È". Символически определение 4 можно записать как формулу

C=AÈB

В логике операции объединения соответствует логическая связка "ИЛИ" (обозначается "Ú"). Если речь идет об объектах со свойствами P или Q, то логическая формула PÚQ означает, что речь идет только об объектах, которым присуще хотя бы одно из этих свойств. При этом допускается, что объекты, которым присущи оба этих свойства, также относятся к этому классу объектов.

Пример 3. Пусть A={a, b, c, d} и P={a, c, f}. Тогда AÈP = {a, b, c, d, f}.

Обратите внимание, что в примере 3 элементы a и c, которые содержатся в каждом из множеств A и B, в объединении C не удваиваются, а содержатся как однократные. В математике и ее приложениях иногда используют множества с кратными элементами (они называются мультимножествами), но нам такие множества не понадобятся. В таких множествах нарушаются некоторые законы обычной алгебры множеств.

Операции дополнения, пересечения и объединения являются основными операциями алгебры множеств.

Определение 5. Разностью множеств A и B называется множество C=A\B, которое содержит только те элементы множества A, которые не являются одновременно элементами множества B.

Пример 4. Пусть A={a, b, c, d} и B={a, c, f}. Тогда A\B = {b, d}.

Важно отметить, что разность множеств является производной операцией. Это означает, что ее можно выразить с помощью других основных операций – для разности множеств справедливо следующее соотношение:

A\B = AÇ.

Если в примере 4 задать универсум, например, U = {a, b, c, d, e, f}, то нетрудно убедиться в справедливости этого равенства:

= {b, d, e}; тогда A\B =AÇ= {b, d}.

В то же время операцию дополнения можно выразить с помощью операции разности: =U\A. В некоторых версиях алгебры множеств операция разности множеств представлена как основная операция, а операция дополнения – как производная операция. Однако основные соотношения (или законы) алгебры множеств при этом остаются неизменными.

На рисунке 3 соответствующие операции над множествами изображены с помощью "кругов Эйлера". Серым цветом показаны результаты операций.

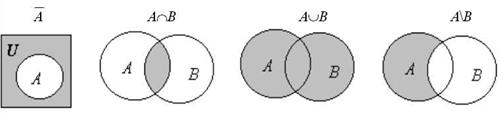
Рис. 3

Здесь хотелось бы обратить внимание на следующее важное обстоятельство. Для множеств A и B, у которых нет общих элементов, справедливы следующие соотношения:

AÇB = Æ ; AÍ; BÍ.

Ситуацию, соответствующую этим соотношениям, можно наглядно отобразить с помощью диаграммы Эйлера (рис. 4).