Контрольная работа: Основные понятия алгебры множеств

Рис. 4

Теперь у нас вполне достаточно понятий для того, чтобы отобразить в виде математической формулировки заданные суждения. Например, суждение "Все члены палаты лордов носят титул пэра" то расчленяется на субъект "члены палаты лордов" (A) и предикат "носят титул пэра" (B). Тогда математической формулой данного суждения будет

AÍB.

Это означает, что все члены палаты лордов включены в множество тех, кто носит титул пэра. Более сложное суждение, например, "Все члены палаты лордов носят титул пэра и находятся в здравом рассудке" можно выразить, используя два предиката: "носят титул пэра" (B) и "находятся в здравом рассудке" (С). Тогда получим следующую математическую формулировку:

AÍ(BÇC).(1)

В случае, когда в суждении имеются предикаты с отрицаниями, используем в математической записи операцию дополнения. Например, суждение "Все члены палаты лордов носят титул пэра и не принимают участия в скачках на мулах", можно записать как

AÍ(B Ç), (2)

где D – предикат "принимают участие в скачках на мулах".

Если использовать диаграммы Эйлера, то получим наглядное изображение формул (1) и (2) (рисунки 5 и 6).

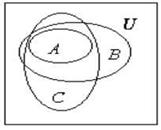
Рис. 5

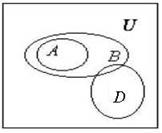
Рис. 6

Количественные соотношения в диаграммах Эйлера (т. е. в данном случае – площади фигур) не принимаются во внимание. Среди наших знаний немало таких, когда не знаем, чему равно число элементов множества, но это не мешает нам знать о том, что некоторые из таких множеств строго включены в некоторые другие множества, или что некоторые из таких множеств точно не содержат общих элементов с некоторыми другими множествами. Количественный анализ множеств во многих случаях является составной частью наших знаний.

В математическую форму суждений можно перевести многие предложения естественного языка.

Законы алгебры множеств – это по сути теоремы, которые выводятся из основных определений и аксиом. Часто приводятся 26 или 28 законов алгебры множеств. Приведем без доказательства лишь некоторые из них, необходимые для ясного понимания дальнейшего. Пусть A, B, C – некоторые произвольные множества в универсуме U. Тогда законами алгебры множеств являются следующие соотношения между ними.

1. =A.

Пример 5. Пусть U={a, b, c, d} и P={a, c}. Тогда ={b, d} и ={a, c}=P.

В алгебре множеств это соотношение (двойное дополнение) носит название закон инволюции. В логике этот закон известен под названием закон отрицания отрицания (или закон двойного отрицания): не (не-A) – то же самое, что и A.

2. A Ç = Æ (множество и его дополнение не имеют общих элементов)

В логике этому закону соответствует закон непротиворечия (утверждение и его полное отрицание логически несовместимы).

3. A È = U.

В логике этому закону соответствует закон исключенного третьего (совмещение любого утверждения и его полного отрицания не допускает присутствия какого-либо третьего промежуточного варианта).

Следующие соотношения характеризуют более подробно свойства пустого множества и универсума:

4. = U;

5. = Æ

6. AÇÆ = Æ;

7. AÈÆ = A;

8. AÇU = A;