Контрольная работа: Основы математики

.

В этом интервале с вероятностью γ = 0,95, будет находиться средняя генеральной совокупности.

Задание № 9

Даны исправленное среднее квадратическое отклонение S, выборочное среднее и объем выборки n нормально распределенного признака генеральной совокупности. Пользуясь распределением Стьюдента, найти доверительные интервалы для оценки генеральной средней , с заданной надежностью γ.

S		n	γ
13	119.5	18	0,99

Решение:

Доверительный интервал, для нормального распределения случайной величины с известным квадратичным отклонением σ, но с известным исправленным средним квадратичным отклонением S, выборочной средней и объемом выборки n и доверительной вероятностью γ, имеет вид.

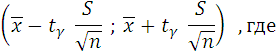
где t_γ = t (γ; n) – коэффициенты Стьюдента, значения n = 18 и γ = 0,99, t_γ = 2,39, то есть t (0,99; 18) = 2,39.

Тогда доверительный интервал:

В интервале (112,16; 126,84) с вероятностью γ = 0,99 будет находиться средняя генеральной совокупности.

Задание № 10

При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты.

эмпирические частоты, ni	3	13	17	45	13	14	5
теоретические частоты, n’i	5	15	14	50	11	12	3

Решение:

В соответствии с критерием согласия х ² (Пирсона) определим наблюдаемое значение критерия:

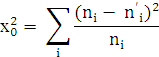
Таким образом, Х_о ² = 2,91, по таблице критических точек распределения при уровне значимости d = 0,05 и числе степени свободы к = m – 3 = 7 – 3 = 4, где m – число различных вариантов выборки, находим: Х_кр ² .

Х_кр ² = х² (0,05; 4) = 8,0

Так как Х_о ² <Х_кр ² , то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.