Контрольная работа: Основы моделирования технологических систем
Зададим свойства материала, граничные условия как показано в нижеприведенном отчете согласно задания.
Таблица 3 — Статистика сетки
| Number of degrees of freedom | 5297 |
| Number of mesh points | 1349 |
| Number of elements | 2600 |
| Triangular | 2600 |
| Quadrilateral | 0 |
| Number of boundary elements | 208 |
| Number of vertex elements | 12 |
| Minimum element quality | 0.842 |
| Element area ratio | 0.216 |
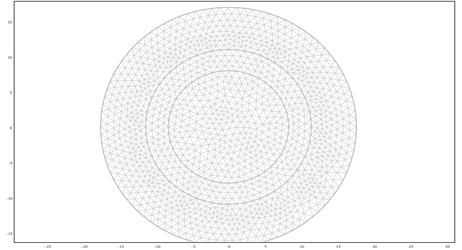
Рисунок 18 — Конечно-элементная сетка
Таблица 4 — Граничные условия
| Boundary | 1-2, 7, 12 | 3-4, 8, 11 | 5-6, 9-10 | |
| Type | Heat flux | Heat flux discontinuity | Temperature | |
| Heat transfer coefficient (h) | W/(m2⋅K) | 5 | 40 | 40 |
| Problem-dependent constant (Const) | W/(m2⋅K4) | 0.5 | 0 | 0 |
| Ambient temperature (Tamb) | K | 0 | 0 | 373 |
| Temperature (T0) | K | 273.15 | 273.15 | 373 |
Таблица 5 — Свойства материалов
| Subdomain | 1 | 2 | 3 | |
| Thermal conductivity (k) | W/(m⋅K) | k(T[1/K])[W/(m*K)] (Compoglass F) | k(T[1/K])[W/(m*K)] (9 Ni steel (UNS K81340)) | k(T[1/K])[W/(m*K)] (Water, liquid) |
| Density (rho) | kg/m3 | rho(T[1/K])[kg/m^3] (Compoglass F) | rho(T[1/K])[kg/m^3] (9 Ni steel (UNS K81340)) | rho(T[1/K])[kg/m^3] (Water, liquid) |
| Heat capacity at constant pressure (C) | J/(kg⋅K) | C(T[1/K])[J/(kg*K)] (Compoglass F) | C_solid_1(T[1/K])[J/(kg*K)] (Aluminum) | Cp(T[1/K])[J/(kg*K)] (Water, liquid) |
| External temperature (Text) | K | 0 | 0 | 0 |
| Subdomain initial value | 1 | 2 | 3 | |
| Temperature (T) | K | 273.15 | 273.15 | 373 |
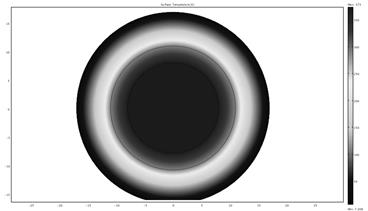
Рисунок 19 — Решение задачи
Задача №4
К свободному краю консольно-закрепленной плоской прямоугольной пластины с отверстием приложена нагрузка F в точке, отмеченной красным. Материал и размеры даны в таблице. Провести моделирование пластины под нагрузкой, определить деформацию пластины и напряжение в материале. Вид на рисунке сверху.
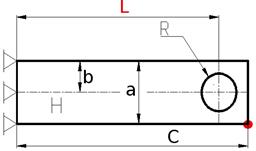
Рисунок 20 — Созданная геометрия
![]()
![]()
Для конструкционного моделирования будем использовать пакет ABAQUS Student Edition, которой является лицензионным при ограничении в 1000 элементов сетки, что должно хватить для нашей задачи. Создадим эскиз и после задания толщины получим трехмерную модель в препроцессоре.
Зададим свойства материалу: плотность серебра 104920 кг/м3, модуль Юнга 71ГПа, коэффициент Пуассона 0,3. Создав сечение балки (section), присвоим материал нашей модели. В модуле Step задаются шаги анализа — у нас статическая задача (Static, General). В модуле Load вводится защемление и ограничение балки. При этом 770 Н направлены вниз. Решение показано на рис. 21.
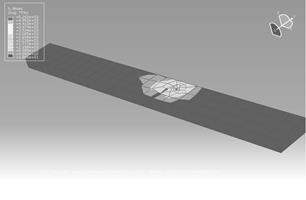
Рисунок 21 — Решение задачи