Контрольная работа: Особенности арифметико-логических устройств (АЛУ) с двоично-десятичными кодами (ДДК) при вычислении операций умножения и деления и поиск путей их ускорения

Особенности АРИФМЕТИКО-ЛОГИЧЕСКИХ УСТРОЙСТВ (АЛУ) с двоично-десятичными кодами (ДДК) при вычислении операций умножения и деления и поиск путей их ускорения

Двоичные коды достаточно громоздкие и поэтому в качестве входной и выходной информации часто используют ДДК. ДДК получают при преобразовании десятичного числа в двоичное путем замены каждой десятичной цифры числа ее двоичным эквивалентом, выделяя при этом под каждую десятичную цифру 4 двоичных разряда. Очевидно, что такие преобразования не соответствуют переводу числа из десятичного формата в двоичный. Однако такой способ является весьма простым. Поэтому, при использовании ДДК чисел необходимо выполнять необходимые корректирующие действия , которые приводят полученное значение к истинному результату.

Пример:

37=

АЛУ, построенное для обработки ДДК базируется на традиционном двоичном сумматоре с выполнением дополнительных корректирующих действий. Основная идея корректирующих механизмов заключается в том, что при обработке десятичных разрядов переносы в смежные разряды возникают при значениях, превышающих число 10, а при сложении ДДК перенос в смежный разряд возникает при превышении в разряде 16. Единицей данных при обработке ДДК является т. наз. тетрада, представляющая собой 4 последовательных бита. Для компенсации искажений, возникающих при сложении ДДК, формируют операнд, каждая цифра которого имеет избыток, равный 6. В таком случае:

z[i]=x[i]+y[i]+P[i]

Если при обработке i-того разряда десятичного кода при сложении i-того разряда первого операнда, i-того разряда второго операнда и входного переноса в i-тый разряд, значение превышает 10, то в i-том разряде остается

z[i]=x[i]+y[i]+P[i]-10

P[i+1]=1

Формируется сигнал переноса в следующий разряд. Поэтому при сложении операндов с избытком в (х6) получаем:

zt=x6+Y

В таком случае в i-том разряде zt будет такое значение:

тогда zt$16. В таком случае в i-том разряде zr будет:

zr[i]=6+x[i]+y[i]+P[i]-16=x[i]+y[i]+P[i]-10=z[i]

P[i+1]=1 –перенос в следующий разряд

При получении псевдосуммы zt обнаруживается ситуация, когда разряды (тетрады), из которых был перенос в старший разряд, содержат правильное значение цифры этого разряда. Разряды, из которых не было переносов в старший разряд, содержат цифру с избытком, равным 6. Поэтому полученное значение требует корректировки. Она может быть проведена путем вычитания из разрядов, из которых не было переносов, значения 6. На практике, вместо вычитания к этим разрядам добавляют значение равное 10 и блокируют межтетрадные переносы:

Упрощенная схема АЛУ

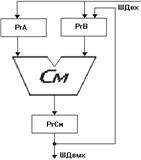
Алгоритм сложения ДДК

РгВ принимает первый операнд, затем в РгА формируют числосо значением 6 в каждой тетраде.

В РгСм формируется код первого операнда с избытком 6, который принимается в РгВ.

В РгА принимается второй операнд. Сумматор формирует значение zr=x6+y. При этом тетрады, из которых не возникли сигналы переноса, фиксируются.

В ргА формируется операнд, в тетрадах которого размещено число 10, если в соответствующих тетрадах zr не возникал сигнал переноса. zr из РгСм передается в РгВ.

Корректировка zr путем добавления операнда с 10 в РгА с блокировкой межтетрадных переносов. Полученный результат передается на выходную шину данных.

Для вычитания ДДК производятся такие действия:

Второй операнд Y преобразуют в обратный код инвертированием каждого бита, при этом получается обратный код с избытком 6, т.к. каждая тетрада является дополнением до 15.

Выполняется суммирование . Если из старшей тетрады zr при формировании был перенос, то получено положительное значение результата. Если переноса не было из старшей тетрады, то результат является отрицательным в дополнительном коде. При этом дополнительный код инвертируется и добавляется 1 к младшему разряду. Полученное значение требует корректировки. Если при получении zr из тетрады был перенос, то в последствии к этой тетраде надо добавить 10 с блокировкой межтетрадных переносов.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--