Контрольная работа: Особенности экономико-математического моделирования

Объемы выборок находятся в соотношении . Тогда из формулы нахождения погрешности

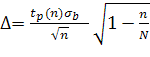(15)

следует, что при возрастании объема выборки n значение Δ уменьшается и Δ1<Δ2, т. е. доверительный интервал, соответствующий объему выборки , будет меньше доверительного интервала, соответствующего объему выборки n2=52.

б)

Исходя из формулы (15) следует, что при возрастании надежности P значение увеличивается, так как увеличивается значение функции Стьюдента tp(n). Следовательно, Δ1>Δ2, т. е. доверительный интервал, соответствующий надежности , будет больше доверительного интервала, соответствующего надежности =0,605

в)

=1,42

Исходя из формулы (15) следует, что при возрастании среднеквадратического отклонения значение Δ увеличивается. Следовательно, Δ1>Δ2, т. е. доверительный интервал, соответствующий среднеквадратическому отклонению σ1=1,58, будет больше доверительного интервала, соответствующего среднеквадратическому отклонению σ2=1,42.

Задание 8. Эконометрические модели. Корреляционные методы

8.1 Дайте понятия функциональной и корреляционной зависимостей

Функциональная зависимость – это такая связь между результативными и факторными признаками, когда значение результативного при-знака-функции полностью определяется значениями факторных признаков.

Корреляционная зависимость – это такая связь между признаками, когда определенным значениям факторных признаков соответствует множество случайных значений результативного признака. Например, зависимость веса человека от роста: множество людей, имеющих одинаковый рост, обладают различным весом.

8.2 Дайте определение коэффициента корреляции. Каковы его смысл и свойства?

Особое место в анализе взаимосвязей между результативным и факторным признаками занимает выявление тесноты связи между ними, которая характеризуется при линейной корреляционной связи коэффициентом корреляции r. Он рассчитывается по формуле

r=b

где σx, σy– среднеквадратические отклонения факторного x и результативного y признаков.

Если r=1, то все точки (), расположены на прямой и связь между признаками y и x самая сильная – функциональная. Если r, то связь называют прямой, т. е. с возрастанием значения факторного признака возрастает значение результативного. При r<0 – связь обратная, т. е. с возрастанием значения факторного признака значение результативного убывает. Таким образом, знак определяет направление связи (прямая, обратная). При r=0 признаки y и x называют некоррелированными.

8.3 Оцените тесноту связи и направление связи между признаками x и y, если известны: b– коэффициент регрессии, σx, σy – среднеквадратические отклонения признаков x и y

Направление и теснота связи между признаками и оцениваются на основе коэффициента корреляции, который рассчитывается по формуле

r=b

В данном случае

b==-0,359

=1,58

=1,42

r=-0,359=-0,400

r=-0,400

Коэффициент корреляции показывает, что связь между признаками x и y умеренная и обратная, т. е. при возрастании факторного признака x значение результативного признака y уменьшается.

Список использованной литературы