Контрольная работа: Парная и множественная регрессия и корреляция

4. Оценка параметров уравнения множественной регрессии

4.1 Оценка параметров с помощью метода определителей

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.

Для оценки параметров уравнения множественной регрессии построим с помощью MS Excel вспомогательную таблицу 2.

Таблица 2 Вспомогательная таблица для расчета параметров уравнения множественной регрессии

№
1	7,2	19,9	9,6	51,8	143,28	396,01	69,12	191,04	92,16
2	8,1	17,1	9,4	65,6	138,51	292,41	76,14	160,74	88,36
3	8,4	17,4	9,6	70,6	146,16	302,76	80,64	167,04	92,16
4	8,6	13,5	8,9	74	116,1	182,25	76,54	120,15	79,21
5	8,6	14,8	10,2	74	127,28	219,04	87,72	150,96	104,04
6	8,4	14,2	8,4	70,6	119,28	201,64	70,56	119,28	70,56
7	9,9	15,1	9,9	98	149,49	228,01	98,01	149,49	98,01
8	10,1	17	10,6	102	171,7	289	107,06	180,2	112,36
9	16,2	14,5	11,9	262	234,9	210,25	192,78	172,55	141,61
10	11,6	16,1	11,9	135	186,76	259,21	138,04	191,59	141,61
11	10,5	14,8	11,6	110	155,4	219,04	121,8	171,68	134,56
12	11,4	12,4	10,9	130	141,36	153,76	124,26	135,16	118,81
13	10,6	12,6	8,3	112	133,56	158,76	87,98	104,58	68,89
14	15,2	15,5	10,3	231	235,6	240,25	156,56	159,65	106,09
15	8,6	20,3	10,7	74	174,58	412,09	92,02	217,21	114,49
16	7,9	17,1	9,7	62,4	135,09	292,41	76,63	165,87	94,09
17	5,8	30,4	11,8	33,6	176,32	924,16	68,44	358,72	139,24
18	8	13,8	17	64	110,4	190,44	136	234,6	289
19	4	44,8	16,7	16	179,2	2007	66,8	748,16	278,89
20	6,6	18,3	12,8	43,6	120,78	334,89	84,48	234,24	163,84
21	4,5	44,2	14,5	20,3	198,9	1953,6	65,25	640,9	210,25
22	6,9	18,3	14,2	47,6	126,27	334,89	97,98	259,86	201,64
23	7,9	12,9	13,6	62,4	101,91	166,41	107,44	175,44	184,96
24	9,8	19,2	11,3	96	188,16	368,64	110,74	216,96	127,69
Итого	214,8	454,2	273,8	2107	3711	10337	2393	5426,07	3252,5
Среднее	8,592	18,2	10,95	84,3	148,44	413,48	95,72	217,043	130,1

На основе расчетов, представленных в таблице 2, получили следующую систему:

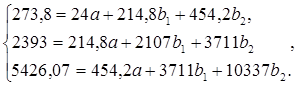
Решаем систему с помощью метода определителей. При этом:

где − определитель системы;

− частные определители.

В результате расчета определителей получили следующие значения:

∆=4702879,56;

∆а=45336681,238, ,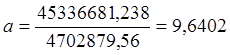

∆b1=–326370,8088, ,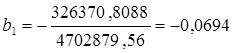

∆b2=593730,7872, .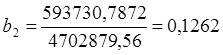

Уравнение множественной регрессии имеет вид:

=9,6402-0,0694х1+0,1262х2.

Таким образом, при увеличении уровня бедности на 1%, общий коэффициент рождаемости в изучаемых регионах снизится на 0,0694 раз, а при увеличении среднедушевого дохода на 1000 руб., общий коэффициент рождаемости увеличится на 0,1262 раз.

4.2 Построение уравнения регрессии в стандартизованном масштабе

Параметры множественной регрессии можно определить другим способом, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

,

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:

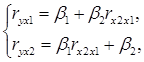
где rух1, rух2 – парные коэффициенты корреляции.

Парные коэффициенты корреляции найдем по формулам:

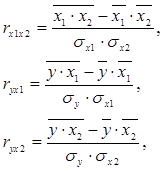
где