Контрольная работа: Парная и множественная регрессия и корреляция
![]()
6.3 Определение коэффициента детерминации (скорректированного, нескорректированного)
Качество построенной модели в целом оценивает коэффициент детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:
![]() .
.
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:
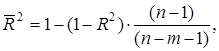
![]()
Таким образом, вариация общего коэффициента рождаемости на 27,9% (21% - при скорректированном индексе детерминации) зависит от вариации уровня бедности и среднедушевого дохода, а на остальные 72,1% (79%) от других факторов, не включенных в модель.
6.4 Частные коэффициенты корреляции
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель. Формула коэффициента частной корреляции, выраженная через показатель детерминации, для х1 принимает вид:
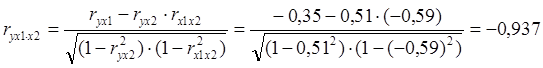 ,
,
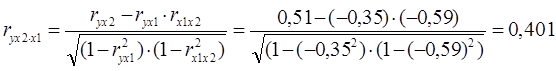 .
.
Таким образом, при закреплении фактора х2 на постоянном уровне (элиминировании) корреляция у и х1 равна -0,937, то есть связь обратная сильная. При закреплении фактора х1 на постоянном уровне корреляция у и х2 равна 0,401, то есть связь прямая слабая.
7. Оценка надежности результатов множественной регрессии и корреляции
7.1 Оценка значимости уравнения с помощью F-критерия Фишера
Значимость уравнения множественной регрессии в целом, оценивается с помощью F-критерия Фишера по формуле:
![]()
При этом выдвигается гипотеза о статистической незначимости уравнения регрессии и показателя тесноты связи.
![]()
Fтабл. =4,32 (при k1=m=2 и k2=n-m-1=24-2-1=21.
Так как Fфакт. < Fтабл, то гипотезу (Н0) принимаем. С вероятностью 95% делаем вывод о статистической не значимости уравнения в целом и показателя тесноты связи, которые сформировались под неслучайным воздействием факторов х1, х2.
7.2 Расчет частных F-критериев
Частные F-критерии оценивают статистическую значимость присутствия факторов х1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. Fх1 оценивает целесообразность включения в уравнение фактора х1 после того, как в него был включен фактор х2. Соответственно, Fx2 указывает на целесообразность включения в модель фактора х2 после фактора х1. Определим частные F-критерии для факторов х1 и х2 по формулам:


Fтабл. = 4,32.
Таким образом, низкое значение Fх1факт. свидетельствует о нецелесообразности включения в модель фактора х1 (уровень бедгости). Включение же фактора х2 в модель статистически целесообразно. Это означает, что парная регрессионная модель зависимости общего коэффициента рождаемости от среднедушевого дохода является достаточно статистически значимой, надежной и нет необходимости улучшать ее, включая дополнительный фактор х1.
7.3 Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента
Частный F-критерий оценивает значимость коэффициентов чистой регрессии: