Контрольная работа: по Эконометрике 3

6 . Для оценки тесноты связи рассчитаем линейный коэффициент парной корреляции:

Коэффициент корреляции, равный 0,9687, показывает, что выявлена весьма тесная зависимость между среднегодовой численностью занятых в экономике и валовым региональным продуктом. Коэффициент детерминации, равный 0,9384, устанавливает, что вариация валового регионального продукта на 93,84% из 100% предопределена вариацией среднегодовой численности занятых в экономике; роль прочих факторов, влияющих на розничный товарооборот, определяется в 6,16%, что является сравнительно небольшой величиной.

7 . Для оценки статистической надёжности выявленной зависимости дохода от доли занятых рассчитаем фактическое значение F -критерия Фишера – F _фактич . и сравним его с табличным значением – F _табл. . По результатам сравнения примем решения по нулевой гипотезе , то есть, либо примем, либо отклоним её с вероятностью допустить ошибку, которая не превысит 5% (или с уровнем значимости α=0,05).
В нашем случае,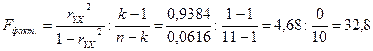

Где k -число факторов в уравнении; n - число изучаемых объектов. Фактическое значение критерия показывает, что факторная вариация результата в 137 раза больше остаточной вариации, сформировавшейся под влиянием случайных причин. Очевидно, что подобные различия не могут быть случайными, а являются результатом систематического взаимодействия оборота розничной торговли и общей суммы доходов населения. Для обоснованного вывода сравним полученный результат с табличным значением критерия: при степенях свободы d.f. 1 =k=1 и d.f. 2 =n-k-1=11-1-1=9 и уровне значимости α=0,05.
В силу того, что нулевую гипотезу о статистической не значимости выявленной зависимости валового регионального продукта от среднегодовой численности занятых в экономике и её параметрах можно отклонить с фактической вероятностью допустить ошибку значительно меньшей, чем традиционные 5%.

Определим теоретические значения результата Y _теор . Для этого в полученное уравнение последовательно подставим фактические значения фактора X и выполним расчёт.

Например, . См. гр. 5 расчётной таблицы. По парам значений Y _теор . и X _факт . строится теоретическая линия регрессии, которая пересечётся с эмпирической регрессией в нескольких точках. См. график 1.

9. Построим теоретическую линю регрессии, которая пересечётся с эмпирической регрессией в нескольких точках.

В нашем случае, скорректированная ошибка аппроксимации составляет 15,776%. Она указывает на невысокое качество построенной линейной модели и ограничивает её использование для выполнения точных прогнозных расчётов даже при условии сравнительно небольшого изменения фактора X (относительно его среднего значения ).

Зависимость ВРП от численности занятых

График№1

Оценку качества модели дадим с помощью скорректированной средней ошибки аппроксимации:
В нашем случае, скорректированная ошибка аппроксимации составляет 15,776%. Она указывает на невысокое качество построенной линейной модели и ограничивает её использование для выполнения точных прогнозных расчётов даже при условии сравнительно небольшого изменения фактора X (относительно его среднего значения ).
Построение логарифмической функции предполагает предварительное выполнение процедуры линеаризации исходных переменных. В данном случае, для преобразования нелинейной функции в линейную введём новую переменную, которая линейно связана с результатом. Следовательно, для определения параметров модели будут использованы традиционные расчётные приёмы, основанные на значениях определителей второго порядка.

Построение логарифмической функции предполагает предварительное выполнение процедуры линеаризации исходных переменных. В данном случае, для преобразования нелинейной функции в линейную введём новую переменную , которая линейно связана с результатом. Следовательно, для определения параметров модели будут использованы традиционные расчётные приёмы, основанные на значениях определителей второго порядка. См. таблицу №4.

Таблица№4

№
А	1	2	3	4	5	6	7	8	9
1	0,056	-2,882	2,000	8,308	-5,765	-12,249	14,249	203,023	69,382
2	0,119	-2,129	2,100	4,531	-4,470	1,550	0,550	0,303	2,680
3	0,138	-1,981	4,300	3,922	-8,516	4,261	0,039	0,001	0,188
4	0,157	-1, 852	5,100	3,428	-9,443	6,623	-1,523	2,318	7,414
5	0,220	-1,514	7,600	2,293	-11,507	12,799	-5,199	27,025	25,314
6	0,287	-1,248	10,500	1,558	-13,107	17,665	-7,165	51,341	234,890
7	0,422	-0,863	18,900	0,744	-16,306	24,722	-5,822	33,901	28,352
8	0,758	-0,277	13,000	0,077	-3,602	35,444	-22,444	503,720	109,288
9	1,008	0,008	43,400	0,000	0,346	40,662	2,738	7,499	13,335
10	1,147	0,137	50,000	0,019	6,857	43,026	6,974	48,632	33,958
11	1,812	0,594	69,000	0,353	41,016	51,397	17,603	309,860	85,715
Итого	6,124	-12,006	225,900	25,234	-24,497	225,900	0,000	1187,624	410,517
Средняя	0,557	-1,091	20,536	—	—	—	—	2,9	10,5
Сигма	0,535	1,050	21,852
Дисперсия, D	0,286	1,103	477,502

Расчёт определителей второго порядка даёт следующие результаты:

; ; .

Отсюда получаем параметры уравнения:

Полученное уравнение имеет вид:

Оценочные показатели позволяют сделать вывод, что линейно-логарифмическая функция описывает изучаемую связь хуже, чем линейная модель: оценка тесноты выявленной связи ρ=0,8798 (сравните с 0,7741), скорректированная средняя ошибка аппроксимации здесь выше и составляет 37,32%, то есть возможности использования для прогноза данной модели более ограничены.
Заключительным этапом решения данной задачи является выполнение прогноза и его оценка.
Если прогнозное значение фактора составит 1,023 от среднего уровня, то есть

X_{прогнозн} .= 1,023*0,557=0,569, тогда прогнозное значение результата сформируется на уровне: Y_{прогнозн} . =39,565-1,491*0,569=38,715 (млрд. руб.).
Рассчитаем интегральную ошибку прогноза - , которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии- и ошибки прогноза положения регрессии. То есть,

Ошибка положения регрессии составит: 0,012 (млрд. руб.).
Интегральная ошибка прогноза составит: 5,976 (млрд. руб.).
Предельная ошибка прогноза, которая не будет превышена в 95% возможных реализаций прогноза, составит: = 2,26*5,976 = 13,506 ≈ 14,0 (млрд. руб.). Табличное значение t-критерия для уровня значимости α=0,05 и для степеней свободы n-k-1 = 11-1-1=7 составит 2,26. Следовательно, ошибка большинства реализаций прогноза не превысит млрд. руб.
Это означает, что фактическая реализация прогноза будет находиться в доверительном интервале .

Верхняя граница доверительного интервала составит
= 38,715 + 14,0 = 52,715(млрд. руб.).
Нижняя граница доверительного интервала составит:

= 38,715 - 14,0 = 24,715(млрд. руб.).
Относительная величина различий значений верхней и нижней границ составит: = раза. Это означает, что верхняя граница в 2,13 раза больше нижней границы, то есть точность выполненного прогноза весьма невелика, но его надёжность на уровне 95% оценивается как высокая. Причиной небольшой точности прогноза является повышенная ошибка аппроксимации. Здесь её значение выходит за границу 5-7% из-за недостаточно высокой типичности линейной регрессии, которая проявляется в присутствии единиц с высокой индивидуальной ошибкой. Если удалить территории с предельно высокой ошибкой (например, Дагестан с ), тогда качество линейной модели и точность прогноза по ней заметно повысятся.

Задача№2.

Производится анализ значений социально-экономических показателей по территориям Северо-Западного федерального округа РФ за 2000 год..

Y – оборот розничной торговли, млрд. руб.;

X ₁ – кредиты, предоставленные в 2000 году предприятиям, организациям, банкам и физическим лицам, млрд. руб.;

X ₂ – доля лиц в высшим и незаконченным высшим образованием среди занятых, %;

X ₃ – годовой доход всего населения, млрд. руб.

Требуется изучить влияние указанных факторов на стоимость валового регионального продукта.

Предварительный анализ исходных данных по 10 территориям выявил наличие двух территорий (г. Санкт-Петербург и Вологодская обл.) с аномальными значениями признаков. Эти территории должны быть исключены из дальнейшего анализа. Значения приводимых показателей рассчитаны без учёта указанных двух аномальных единиц.

При обработке исходных данных получены следующие значения: