Контрольная работа: Построение порождающего полинома циклического кода по его корням (степеням корней)
4. Поле всегда содержит мультипликативную единицу 1, так что ![]() и аддитивную единицу 0, так что
и аддитивную единицу 0, так что ![]() .
.
5. Для умножения и сложения выполняются правила ассоциативности, коммутативности и дистрибутивности.
1.4 Поля Галуа
Конечное поле или поле Галуа – это поле (далее конечное поле обозначено, как GF(p)), содержащее конечное число элементов. Нужно отметить, что аксиомы 1 – 5, справедливы, как для поля с конечным числом элементов, так и с бесконечным, но главное отличие конечных полей от бесконечных определяет аксиома 2. Из этого вытекает, что на понятие «умножение» и «сложение» накладывается ряд ограничений. Выполнение аксиомы 2 осуществляется выполнением по модулю некоторого числа p, называемым характеристикой поля.
Конечные поля существуют не при любом числе элементов, а только когда количество элементов поля – простое число pили его степень pm , где m – целое положительное число. В первом случае поле называется простым и обозначается, как GF(p), а во втором называется расширением простого поля и обозначается GF(pm ) .
Рассмотрим некоторое поле GF(p). Такое поле содержит p элементов, операции сложения и умножения над элементами этого поля производятся по модулю числа p. Рассмотрим расширение этого поля - GF(pm ). Элементами ![]() расширения поля будут являться полиномы степени
расширения поля будут являться полиномы степени ![]() и меньше, с коэффициентами из поля GF(p). Приведем аналогию - простое поле содержит буквы алфавита, а расширение этого поля содержит слова определенной длины, составленные по некоторым правилам из букв, лежащих в основном поле.
и меньше, с коэффициентами из поля GF(p). Приведем аналогию - простое поле содержит буквы алфавита, а расширение этого поля содержит слова определенной длины, составленные по некоторым правилам из букв, лежащих в основном поле.
1.4.1 Примитивный элемент поля и циклическая группа
Основное свойство конечных полей – это связь между собой ненулевых элементов поля ![]() и возможность их выражения через степень элемента
и возможность их выражения через степень элемента ![]() , называемого примитивным, это означает, что любой элемент поля можно представить, как степень примитивного элемента, т.е.
, называемого примитивным, это означает, что любой элемент поля можно представить, как степень примитивного элемента, т.е. ![]() и т.д. Множество
и т.д. Множество ![]() элементов расширения поля образуют циклическую мультипликативную группу. Это означает, что все элементы расширения находятся в следующем отношении:
элементов расширения поля образуют циклическую мультипликативную группу. Это означает, что все элементы расширения находятся в следующем отношении: ![]() . Таким образом, умножая элемент
. Таким образом, умножая элемент ![]() на себя можно получить любой элемент расширения поля (мультипликативность), но очевидно, что правило умножения должно быть специфическим, иначе, невозможно обеспечить нужную степень полинома и обеспечить цикличность, т.е. после
на себя можно получить любой элемент расширения поля (мультипликативность), но очевидно, что правило умножения должно быть специфическим, иначе, невозможно обеспечить нужную степень полинома и обеспечить цикличность, т.е. после ![]() умножений начнется повторение.
умножений начнется повторение.
Правило умножения в расширении поля аналогично правилу умножения многочленов с последующим приведением по модулю некоторого специального полинома ![]() степени m. Приведение означает деление результата умножения на полином
степени m. Приведение означает деление результата умножения на полином ![]() и использованию только остатка от деления, нужно отметить, что при делении сложение производится по правилам для основного поля, т.е. сложение проводится по модулю числа p.
и использованию только остатка от деления, нужно отметить, что при делении сложение производится по правилам для основного поля, т.е. сложение проводится по модулю числа p.
Выше было сказано, что полином ![]() должен быть специальным, это означает, что любые операции, выполняемые по модулю
должен быть специальным, это означает, что любые операции, выполняемые по модулю ![]() должны оставаться обратимыми, иначе система не образует поле. Таким образом, полином
должны оставаться обратимыми, иначе система не образует поле. Таким образом, полином ![]() должен быть неприводимым в поле GF(p), т.е. его нельзя разложить на множители, используя только многочлены с коэффициентами из поля GF(p). Аналогом неприводимого полинома является простое число. На сегодняшний день не существует систематического способа поиска неприводимых полиномов. Наиболее обширная таблица неприводимых полиномов представлена в книге [1].
должен быть неприводимым в поле GF(p), т.е. его нельзя разложить на множители, используя только многочлены с коэффициентами из поля GF(p). Аналогом неприводимого полинома является простое число. На сегодняшний день не существует систематического способа поиска неприводимых полиномов. Наиболее обширная таблица неприводимых полиномов представлена в книге [1].
Резюме: Расширение поля содержит полиномы степени m-1 и меньше, с коэффициентами из основного поля. Любой элемент расширения поля можно получить, как степень примитивного элемента ![]() . Умножение проводится по модулю неприводимого над полем GF(p) полиномом. Описанная выше теория может показаться запутанной, но ниже будет дан пример, который поможет понять изложенные теоретические сведения.
. Умножение проводится по модулю неприводимого над полем GF(p) полиномом. Описанная выше теория может показаться запутанной, но ниже будет дан пример, который поможет понять изложенные теоретические сведения.
1.4.2 Модульная арифметика и деление полиномов
Рассмотрим, сложение и умножение по модулю некоторого числа p, это означает проведение операции по обычным правилам, а затем деление результата на число p. Например, умножим 7 на 3 по модулю 10. Обозначим проведение операции по модулю, как «mod» ![]() .
. ![]() Теперь получившийся результат, разделим на 10 и возьмем остаток, остаток равен единице, следовательно
Теперь получившийся результат, разделим на 10 и возьмем остаток, остаток равен единице, следовательно ![]() . Но так как, для работы с двоичными циклическими кодами нам понадобится конечное поле GF(2), которое содержит два элемента – нуль и единицу, то рассмотрим сложение по модулю два. Сумма по модулю два обозначается знаком
. Но так как, для работы с двоичными циклическими кодами нам понадобится конечное поле GF(2), которое содержит два элемента – нуль и единицу, то рассмотрим сложение по модулю два. Сумма по модулю два обозначается знаком ![]() .
.
1![]() 1 = 0
1 = 0
1![]() 0 = 1
0 = 1
0![]() 0 = 0
0 = 0
0![]() 1 = 1
1 = 1
Нетрудно убедиться, что если сложить две единицы и разделить на два, то остаток от деления будет равен нулю, а если сложить единицу с нулем и разделить на два, то остаток будет равен единице.
Деление полиномов .
Положим, что коэффициенты в полиномах лежат в поле GF(2), следовательно, все операции будут проводиться по модулю два. Рассмотрим деление полинома ![]() на полином
на полином ![]() . Алгоритм деления аналогичен простому делению многочлена на многочлен в столбик, с той лишь разницей, что вычитание на каждом шаге деления будет заменено суммой по модулю два.
. Алгоритм деления аналогичен простому делению многочлена на многочлен в столбик, с той лишь разницей, что вычитание на каждом шаге деления будет заменено суммой по модулю два.
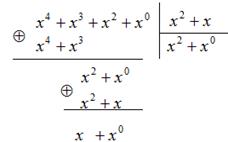
Рассмотрим деление пошагово:
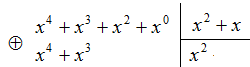
Не трудно убедиться, что на первом шаге делимое можно взять два раза, то есть умножить делимое на ![]() :
: ![]() . Теперь если сложить
. Теперь если сложить ![]() и
и ![]() по модулю два, то так как
по модулю два, то так как ![]() присутствует в обоих операндах, то эти элементы сокращаются, так как они одинаковые. Итак, результат первого шага деления:
присутствует в обоих операндах, то эти элементы сокращаются, так как они одинаковые. Итак, результат первого шага деления:
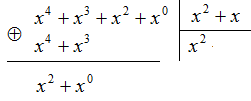
Далее нужно взять делитель один раз, т.е. умножить его на ![]() и сложить результат по модулю два с результатом предыдущего шага. Таким образом, получим:
и сложить результат по модулю два с результатом предыдущего шага. Таким образом, получим:

Итак, ![]() - частное от деления, а
- частное от деления, а ![]() - остаток.
- остаток.
Умножение полиномов.