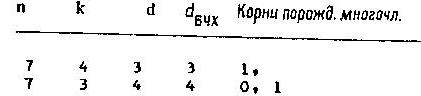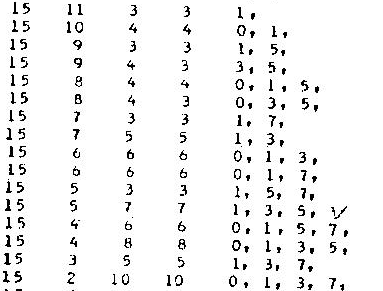Контрольная работа: Построение порождающего полинома циклического кода по его корням (степеням корней)

Для корня со степенью 1:

Для корня со степенью 3: m₃ (x) = (x – a³ ) (x – a⁶ ) (x – a⁹ ) (x – a¹² ) = x⁴ + x³ + x² + x¹ +1.

Для корня со степенью 5: m₅ (x) = (x – a⁵ ) (x – a¹⁰ ) = x² + x+1

Шаг 4. Нахождение порождающего полинома.

Из 1.5 , где это минимальные полиномы для заданных корней, то было получено, что

Заключение

В данной работе рассмотрено краткое математической описание циклических кодов с точки зрения алгебры конечных полей, которого вполне достаточно для решения задачи нахождения порождающего полинома кода, используя его корни. Безусловно, материал изложен в очень сжатой форме и многое нужно принять, как аксиому. Изначально данная работа задумывалась, как описание алгоритма нахождения полинома с некоторыми комментариями к каждому шагу, но в процессе описания алгоритма, оказалось, что без краткой теории конечных полей это сделать невозможно.

Список литературы

1. У. Питерсон, Э. Уэлдон. «Коды, исправляющие ошибки»: Москва: Мир, 1976.

2. Р. Блейхут. «Теория и практика кодов исправляющих ошибки»: Москва: Мир, 1986. - 576с.

3. Жуков А.Б. , Каменский С.В. Передача сообщений. – НГТУ, 2003.

Приложения

Приложение А. Таблица неприводимых полиномов над GF(2).

Приложение Б. Таблица двоичных некоторых циклических кодов тривиальной длины