Контрольная работа: Потрійний інтеграл

1. Поняття потрійного інтеграла. Умови його існування та властивості

Схема побудови потрійного інтеграла така сама, як і звичайного визначеного інтеграла та подвійного інтеграла.

Нехай функція визначена в обмеженій замкненій області . Розіб'ємо область сіткою поверхонь на частин , які не мають спільних внутрішніх точок і об'єми яких дорівнюють . У кожній частині візьмемо довільну точку і утворимо суму

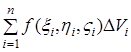,(1)

яка називається інтегральною сумою для функції за областю . Нехай – найбільший з діаметрів областей .

Якщо інтегральна сума (1) при має скінченну границю, яка не залежить ні від способу розбиття області на частини , ні від вибору в них точок , то ця границя називається потрійним інтегралом і позначається одним із таких символів:

або .

Таким чином, за означенням

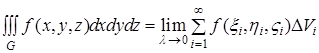,(2)

де – функція, інтегровна в області ; – область інтегрування; і – змінні інтегрування; (або ) – елемент об'єму.

Якщо по тілу розподілено масу з об'ємною густиною в точці , то маса цього тіла знаходиться за формулою

.(3)

Формула (3) аналогічна формулі (1.8) і може розглядатися як механічний зміст потрійного інтеграла, коли підінтегральна функція невід'ємна в області . Якщо всюди в області покласти , то з формули (2) випливає формула для обчислення об'єму тіла :

.(4)

Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.

Теорема (достатня умова інтегровності функції). Якщо функція неперервна в обмеженій замкненій області , то вона в цій області інтегрована.

Властивості потрійних інтегралів.

1. Сталий множник можна винести за знак потрійного інтеграла:

.

Потрійний інтеграл від суми кількох інтегровних функцій дорівнює сумі потрійних інтегралів від доданків:

.

3. Якщо в області інтегрування , то

.

4. Якщо функції та визначені в одній і тій самій області і , то

.

5. (Адитивність потрійного інтеграла.) Якщо область інтегрування функції розбити на частини і , які не мають спільних внутрішніх точок, то

.

6. (Оцінка потрійного інтеграла.) Якщо функція неперервна в обмеженій замкненій області , яка має об'єм , то

,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--