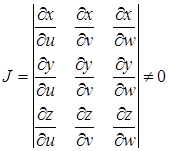Контрольная работа: Потрійний інтеграл

7. (Середнє значення функції.) Якщо функція неперервна в обмеженій замкненій області , яка має об'єм , то в цій області існує така точка , що

.

Величина

називається середнім значенням функції в області .

2. Обчислення потрійного інтеграла

Обчислення потрійного інтеграла зводять до обчислення повторних, тобто до інтегрування за кожною змінній окремо.

Нехай область обмежена знизу і зверху поверхнями і , а з боків циліндричною поверхнею, твірні якої паралельні осі . Позначимо проекцію області на площину через (рис. 1) і вважатимемо, що функції і неперервні в .

Рисунок 1 – Область

Якщо при цьому область є правильною, то область називається правильною у напрямі осі . Припустимо, що кожна пряма, яка проходить через кожну внутрішню точку паралельно осі , перетинає межу області у точках і . Точку назвемо точкою входу в область , а точку – точкою виходу з області , а їхні аплікати позначимо відповідно через і . Тоді , і для будь-якої неперервної в області функції має місце формула

.(5)

Зміст формули (5) такий. Щоб обчислити потрійний інтеграл, потрібно спочатку обчислити інтеграл за змінною , вважаючи та сталими. Нижньою межею цього інтеграла є апліката точки входу , а верхньою – апліката точки виходу . Внаслідок інтегрування отримаємо функцію від змінних та .

Якщо область , наприклад, обмежена кривими і , де і – неперервні функції, тобто

, то, переходячи від подвійного інтеграла до повторного (п. 1.3), отримаємо формулу

,(6)

яка зводить обчислення потрійного інтеграла до послідовного обчислення трьох визначених інтегралів. Порядок інтегрування може бути й іншим, тобто змінні і у правій частині формули (6) за певних умов можна міняти місцями.

Якщо, наприклад, область правильна в напрямі осі :

,

де – неперервні функції, то

.

Зокрема, якщо областю інтегрування є паралелепіпед:

,

то

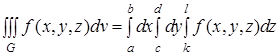.(7)

У цьому разі інтегрування виконується в будь-якому порядку, оскільки область правильна у напрямі всіх трьох координатних осей .

3. Заміна змінних в потрійному інтегралі

Заміну змінної в потрійному інтегралі виконують за таким правилом: якщо обмежена замкнена область взаємно однозначно відображується на область за допомогою неперервно диференційовних функцій , , , якобіан в області не дорівнює нулю: