Контрольная работа: Потрійний інтеграл

. (8)

На практиці найуживанішими є циліндричні та сферичні координати. При переході від прямокутних координат до циліндричних (рис.4, а), пов'язаних з співвідношеннями

;

,

якобіан перетворення

.

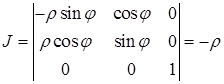З формули (8) отримуємо потрійний інтеграл у циліндричних координатах:

.(9)

Назва «циліндричні координати» пов'язана з тим, що координатна поверхня є циліндром, прямолінійні твірні якого паралельні осі .

При переході від прямокутних координат до сферичних

(рис. 4, б), які пов'язані з формулами

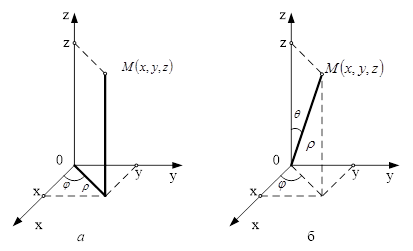
Рисунок 4 – Координати: а) циліндричні; б) сферичні

;

,

якобіан перетворення

.

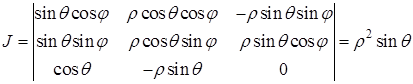З формули (8) знаходимо потрійний інтеграл у сферичних координатах:

. (10)

Назва «сферичні координати» пов'язана з тим, що координатна поверхня є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область , як правило, не будують, а межі інтегрування знаходять безпосередньо за областю , користуючись геометричним змістом нових координат. При цьому рівняння поверхонь та , які обмежують область , записують у нових координатах.

Зокрема, якщо область обмежена циліндричною поверхнею та площинами , то всі межі інтегрування в циліндричній системі координат сталі:

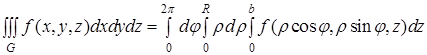
і не змінюються при зміні порядку інтегрування. Те саме буде у сферичних координатах у випадку, коли – куля: або кульове кільце. Наприклад, якщо – кульове кільце з внутрішньою сферою , то рівняння цієї сфери в сферичних координатах має вигляд

або

,

звідки . Аналогічно – рівняння зовнішньої сфери, тому

.

У випадку, коли – куля , у цій формулі слід покласти . Інших будь-яких загальних рекомендацій, коли необхідно переходити до тієї чи іншої системи координат, дати неможливо. Це залежить і від області інтегрування, і від підінтегральної функції. Іноді потрібно написати інтеграл у різних системах координат і лише після цього вирішити, в якій з них обчислення буде найпростішим.