Контрольная работа: Проблема дискретного логарифмування

В пошуках криптографічних алгоритмів з відкритим розповсюдженням ключів з експоненціальною складністю криптоаналізу спеціалісти зупинилися на криптографічних перетвореннях, що виконуються в групі точок ЕК.

Відповідно до прогнозів ці перетворення ще довго забезпечуватимуть необхідний рівень стійкості. Розглянемо основні задачі криптоаналізу для систем, в яких перетворення здійснюються в групі точок ЕК, методи їх розв'язання та дамо оцінку стійкості для відомих нам методів криптоаналізу.

Під час аналізу стійкості необхідно розглянути дві проблеми стійкості – розв’язання задачі дискретного логарифму та задачі Діффі-Хеллмана.

Проблема дискретного логарифму формується у наступному вигляді. Нехай задано точку на еліптичній кривій , де (просте число) або (просте число, натуральне, ). Відомо також значення відкритого ключа , причому

. (1)

Необхідно знайти конфіденційний (особистий ) ключ .

Проблема Діффі – Хеллмана формується у наступному вигляді. Нехай дано ЕК , відомо значення точки , а також відкритий ключ . Необхідно знайти загальний секрет

, (2)

де та – особисті ключі відповідно першого та другого користувачів.

Насьогодні для аналізу стійкості та проведення криптоаналізу знайшли розповсюдження декілька методів Полларда - та оптимальний .

Поллард запропонував замість детерміністського псевдоймовірнісний алгоритм розв’язання в полі .

Це дозволило істотно знизити вимоги до обсягу пам'яті при практично тій же стійкості алгоритму. Ідея методу заснована на випадковому пошуку двох співпадаючих точок серед точок криптосистеми.

У теорії ймовірностей добре відомі задачі про випадкові блукання. Одна із задач ставиться так. Є ящиків і куль, які випадково розміщені по ящиках.

Процедура закінчується при першому влученні кулі у вже зайнятий ящик. Потрібно визначити медіану розподілу ймовірностей

Більш простою моделлю є задача про співпадаючі дні народження. Якщо - число днів у році, то скільки чоловік з рівноймовірними днями народження в році потрібно відібрати, щоб з імовірністю дні народження хоча б двох чоловік збіглися?

Очевидно, що ймовірність такої події дорівнює

При неважко отримати наближене значення цієї імовірності

Приймаючи , отримаємо оцінку числа . Інакше кажучи, щоб при випадковому переборі великої множини із чисел з імовірністю 50% двічі з'явилося те саме число, буде потрібно в середньому порядку спроб. Збіг елементів або точок в аналізі прийнято називати колізією. Нехай , де генератор криптосистеми має великий простий порядок . Алгоритм - методу в застосуванні до еліптичних кривих полягає в послідовному обчисленні точок

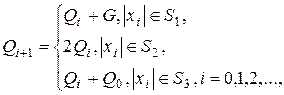
де - якась міра координати точки - три рівноймовірні області, у які може потрапити ця міра. Виберемо випадкові значення й визначимо початкову точку як Ітераційна послідовність обчислень дає послідовність , таку що

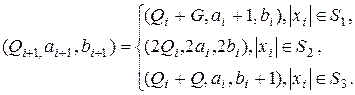
На кожному кроці обчислене значення порівнюється з попереднім аж до збігу (колізії) або

.

Алгоритм разом з колізією дозволяє скласти рівняння

з якого визначається значення дискретного логарифма

.

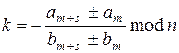--> ЧИТАТЬ ПОЛНОСТЬЮ <--