Контрольная работа: Проблема дискретного логарифмування

Для всіх точок задано операції додавання та подвоєння. Наприклад, якщо а , то

,

Рисунок 2 - Графічна інтерпретація -методу Полларда

де

(4)

Для ЕК над полем виду

причому , то для двох точок та таких, що

виходить

(5)

примітивний поліном m -го степеня;

(6)

Для розв’язання задачі пошуку конфіденційного ключа в порівнянні (1) розглянемо метод Полларда над простимо полем Нехай – базова точка, відкритий ключ, шукатимемо пари цілих та , таких що

(7)

Позначимо в загальному вигляді

(8)

Суть -методу Полларда розв’язання порівняння (1) міститься в наступному. Знайдемо деяку функцію , вибравши де порядок точки на ЕК

(9)

Далі знайдемо послідовність:

...,

для пар , таких що:

(10)

Рекомендується в простих випадках (при відносно невеликих ) послідовність розраховувати у вигляді:

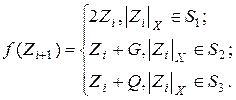(11)

При цьому та складають частини області . Якщо область рівномірно ділиться, то (8.11) має вигляд: