Контрольная работа: Проблема дискретного логарифмування

Це обумовлено детермінованістю алгоритму. Його називають імовірнісним лише у зв'язку з непередбачуваністю шляху, за яким виконується одне із трьох обчислень.

Q ₀ Q ₁ Q ₂ Q_m

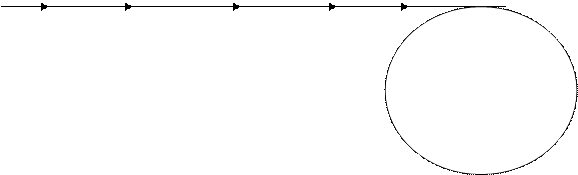
Q_{m +1}

Qm+s-1

Рисунок 1 - Графічна інтерпретація -методу Полларда

Реалізація методу пов'язана з нарощуванням пам'яті, у яку записуються -координати точок, що обчислюють. У міру збільшення порядку криптосистеми він незабаром стає практично нереалізованим. Позбутися від цього недоліку вдається за допомогою методу Флойда. Ідея методу проста й елегантна.

На циферблаті секундна стрілка завжди обганяє хвилинну, а хвилинна - годинну. При влученні всередину петлі в -методі Полларда якась точка наздоганяє точку (колізія ), що дає рішення ECDLP . У такий спосіб замість порівняння чергової обчисленої точки з усіма попередніми достатньо у пам'яті зберегти для порівняння лише дві точки: і .

Точка колізії при цьому зрушується усередину петлі на відстань, що не перевищує половини довжини петлі. Тим самим відбувається обмін необхідної пам'яті на час обчислень.

Кожен цикл у методі Флойда вимагає обчислення трьох точок відповідно до алгоритму й порівняння двох з них. Вихідні дані – точки й , обчислені в попередньому циклі. Тоді на їхній основі розраховуються точки й і рівняються - координати першої й останньої точок. При їхньому збігу має місце колізія , де знак визначається з порівняння - координат обчислених точок.

Найпростіша ілюстрація цього методу - спрощений алгоритм із обчисленням . Колізія на -му циклі відразу дає розв’язання дискретного логарифму

По суті це прямий метод визначення дискретного логарифму з експоненційною складністю .

В іншому окремому випадку алгоритму маємо

Колізія на -му кроці призведе до рівняння

або

Воно не має розв'язку . Якщо модернізувати алгоритм так, що на кожній ітерації порівнювати точки й генератор , то при виконанні можна отримати розв’язання за умови, що 2 є примітивним елементом поля . Цей метод також вимагає об'єму обчислень порядку

Розглянуті дві частки випадку оцінюються максимальною складністю у зв'язку з тим, що при переборі всіх точок криптосистеми колізія виникає лише один раз.

Перехід до псевдовипадкового алгоритму породжує множина можливих точок колізій, число яких оцінюється як , а обчислювальна складність методу -Полларда, застосованого до групи загальної структури, дорівнює . Оскільки в групі точок EK зворотні точки визначаються досить просто, об'єм пошуку в просторі точок скорочується вдвічі, а обчислювальна складність зменшується в раз і стає рівною

На практиці для виявлення колізій замість методу Флойда знайшла застосування його модифікація, запропонована Шнором і Ленстрой. У цієї модифікації пам'ять містить 8 осередків, зрушення вмісту яких здійснюється при , де - номери ітерацій в останньому й першому осередках відповідно. Отримано експериментальну оцінку складності цього методу для групи

Алгоритм - методу Полларда з розбивкою на три області є споконвічним і найбільш простим у реалізації. Подальші вдосконалення алгоритму пропонують використання рівноймовірних областей з вибором, наприклад, ітераційної функції

Число областей, як правило, не перевищує 20, тому що подальше їхнє збільшення практично не впливає на статистичні характеристики алгоритму.

Очевидно колізію точок можна отримати й іншим шляхом, рухаючись із двох (або більше) різних точок і до збігу . Ця ситуація відображується на рисунку 2. Даний метод одержання колізії зветься -Методом Полларда. Походження терміна прийнято з рисунка.

Розглянемо -метод Полларда на прикладі ЕК над простим полем Галуа , тобто

криптографичний дискретний логарифм