Контрольная работа: Психометрическое обоснование диагностических методик
Теоретическая справка
Под надежностью теста понимается степень точности, с которой тест измеряет определенное свойство или качество. Надежность теста – это характеристика точности его как измерительного инструмента, его устойчивость к действию помех (как внешних, так и внутренних). Эмпирическое определение надежности теста является обязательным условием его допуска для использования в практической деятельности психолога.
Задание 3. Расчет коэффициентов надежности
Цель задания: овладение приемами расчета коэффициентов надежности заданий при помощи расщепления теста на две части (надежность частей теста).
Оснащение: микрокалькулятор, таблица первичных результатов (таблица №3).
Таблица №3
Первичные результаты исследования с помощью теста Равена (n=36, N=80).
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| fi | 78 | 80 | 77 | 79 | 80 | 76 | 60 | 56 | 63 | 70 | 58 | 45 | 79 | 80 | 68 | 50 | 72 | 41 |
| Номер задачи | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| fi | 33 | 44 | 26 | 44 | 12 | 27 | 73 | 65 | 41 | 52 | 37 | 14 | 22 | 15 | 49 | 18 | 27 | 8 |
Порядок работы:
1
. Разделить задачи из Таблицы №3 на две части – нечетные (X) и четные (Y).
2. Вычислить средние арифметические для каждой части (
). Результаты вычислений занесите в следующую таблицу:
Вычисляем средние арифметические для каждой части ().
| Хi | Хi –  | (Хi – )2 | Yi | Yi –  | (Yi – )2 | (Хi – ) (Yi –) | |
| 1 | 78 | 25 | 625 | 80 | 32 | 1024 | 800 |
| 2 | 77 | 24 | 576 | 79 | 31 | 961 | 744 |
| 3 | 80 | 27 | 729 | 76 | 28 | 784 | 756 |
| 4 | 60 | 7 | 49 | 56 | 8 | 64 | 56 |
| 5 | 63 | 10 | 100 | 70 | 22 | 484 | 220 |
| 6 | 58 | 5 | 25 | 45 | -3 | 9 | -15 |
| 7 | 79 | 26 | 676 | 80 | 32 | 1024 | 832 |
| 8 | 68 | 15 | 225 | 50 | 2 | 4 | 30 |
| 9 | 72 | 19 | 361 | 41 | -7 | 49 | -133 |
| 10 | 33 | -20 | 400 | 44 | -4 | 16 | 80 |
| 11 | 26 | -27 | 729 | 44 | -4 | 16 | 108 |
| 12 | 12 | -41 | 1681 | 27 | -21 | 441 | 861 |
| 13 | 73 | 20 | 400 | 65 | 17 | 289 | 340 |
| 14 | 41 | -12 | 144 | 52 | 4 | 16 | -48 |
| 15 | 37 | -16 | 256 | 14 | -34 | 1156 | 544 |
| 16 | 22 | -31 | 961 | 15 | -33 | 1089 | 1023 |
| 17 | 49 | -4 | 16 | 18 | -30 | 900 | 120 |
| 18 | -26 | 676 | 8 | -40 | 1600 | 1040 | |
| =53 | ∑ =8629 | =48 | ∑ =9926 | ∑ =7358 |
= 955/18=53 = 864/18= 48;
3. Вычислить стандартные отклонения для каждой части (
, 
) по формуле:
,
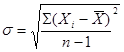где
- разность между значениями варианты и средней арифметической величиной нечетной и четной частей теста, 
- количество задач в нечетной и четной частях теста.
Вычисляем стандартные отклонения для каждой части (, ) по формуле:
,
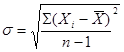n – количество задач в нечетной и четной частях теста = 18
(для нечетной части теста)= ,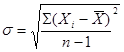
22,5
( для четной части) = 
= 
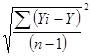= 24,1624,2
4. Вычислить коэффициент полной корреляции между частями теста используя формулу
Пирсона:
,
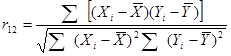где- разность между значениями варианты и средней арифметической величиной нечетной части теста, 
- разность между значениями варианты и средней арифметической величиной четной части теста.
Вычисляем коэффициент полной корреляции между частями теста используя формулу
Пирсона:
, =
= 
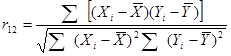= 0,7950,8
0,8 коэффициент полной корреляции между частями теста.
5. Вычислить коэффициенты надежности, используя следующие формулы: