Контрольная работа: Расчет электрических цепей синусоидального тока
110·3.5·sin(-170 )=113.23вар,
где j — угол между векторами тока и напряжения.
Проверка баланса напряжений показывает, что задача решена правильно:
В
Угол между током и напряжением определяем, сравнивая комплексы напряжений 
и тока 
:
В, 
А, 
-170 , 
0.956.
При построении векторной диаграммы на комплексной плоскости считаем, что потенциал точки е равен 0. Тогда из точки е , помещенной в начало координат, под углом -170 относительно вещественной оси в выбранном масштабе строим вектор UR 3 . Конец этого вектора будет определять потенциал точки д. Под углом -1070 к вещественной оси строим вектор UC 2 определяя потенциал точки г . Из точки г под углом 730 строим вектор UL 2 , определяя потенциал точки в . Из точки в строим вектор напряжения UR 2 , определяя потенциал точки б . Из точки б строим вектор напряжения UR 1 , определяя потенциал точки а . Конец вектора UR 1 должен определять потенциал точки а , которая должна лежать на вещественной оси, а длина отрезка еа в соответствии с выбранным масштабом должна быть равной U=110 В.
Задача 2
Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников, схема которой изображена на рис. 2. Дано: U = 380B, L0 = 19мГн, R0 = 8Oм, L1 = 25,5мГн, R1 = 6Oм, R2 = 10Oм, С2 = 396 мкФ.
Определить общий ток цепи 
и токи в ветвях 
и 
, напряжения на участках цепи, активную, реактивную и полную мощности, построить потенциальную диаграмму на комплексной плоскости.
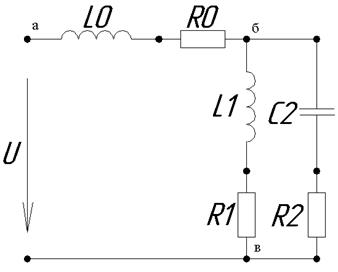
Рис. 2
Решение. Определяем реактивные сопротивления цепи:
Ом
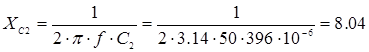Ом
Ом
Выражаем сопротивление ветвей цепи в комплексном виде:
Ом
Ом
Ом
Перевод комплексных чисел в показательную форму не обязателен, но при умножении и делении комплексных чисел показательная форма записи удобнее.
Находим эквивалентное сопротивление параллельных ветвей:
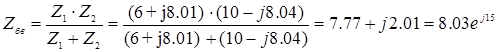Ом
Схема рассчитываемой цепи теперь имеет вид цепи с последовательным соединением приемников.
Комплексное сопротивление всей цепи:
Ом
Определим ток в неразветвленной цепи. Для этого выразим приложенное к цепи напряжение 
в комплексной форме. Так как в условии задачи начальная фаза напряжения не задана, принимаем ее равной нулю, располагая тем самым вектор напряжения с вещественной осью комплексной плоскости:
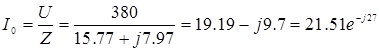А
Определяем комплексное действующее значение на разветвленном участке цепи: