Контрольная работа: Расчет величины прожиточного минимума
Вычислив параметры, получим следующее уравнение:
ух = 1059,5 + 71,1 ∙ х.
Следовательно, с увеличением номера квартала на 1%, величина прожиточного минимума увеличится на 71,1%.
3. Значимость коэффициентов регрессии проверим по t-критерию Стьюдента. Вычислим расчетные значения t-критерия по формулам:
для параметра а0 :
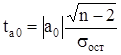 , (5)
, (5)
для параметра а1 :
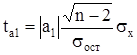 , (6)
, (6)
где n= 20 - объем выборки,
среднее квадратическое отклонение результативного признака у от выровненных значений ух :
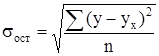 , (7)
, (7)
среднее квадратическое отклонение факторного признака х от общей средней ![]() :
:
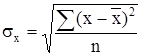 . (8)
. (8)
Находим:
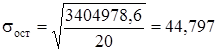 ,
, 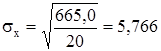 ,
,
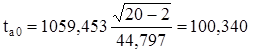 ,
, 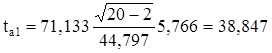 .
.
Вычисленные значения ta 0 и ta 1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 20-2 =18. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым при условии, если tрасч > tтабл .
Так как tрасча0 = 100,340 и tрасча1 = 38,847 больше tтабл = 2,101, то параметры а0 и а1 признаются значимыми, т.е. в этом случае маловероятно, что найденное значение параметра обусловлено только случайными совпадениями.
Выявим тесноту корреляционной связи между х и у с помощью линейного коэффициента корреляции, используя формулу:
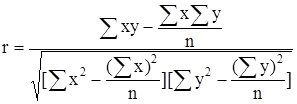 .(9)
.(9)
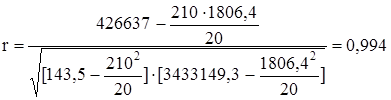 .
.
Т.к. r =0,994, то связь прямая сильная, полная.
Значимость линейного коэффициента корреляции определяется помощью t-критерия Стьюдента (число степеней свободы равно 18, уровень значимости а=0,05) по формуле:
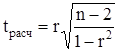 . (10)
. (10)
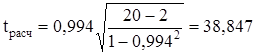 .
.
Так как ![]() = 38,847 больше tтабл = 2,101, следовательно, коэффициент корреляции признается значимым.
= 38,847 больше tтабл = 2,101, следовательно, коэффициент корреляции признается значимым.
Определим линейный коэффициент детерминации r2 :
r2 = 0,9942 = 0,988.
Он показывает, что 98,8% вариации величины прожиточного минимума обусловлено вариацией номера квартала.