Контрольная работа: Расчет величины прожиточного минимума

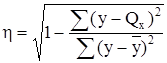. (11)

.

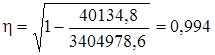Т.к. r = η, то линейная форма связи между у и х выбрана верно. Экономическую интерпретацию модели дополнит коэффициент эластичности:

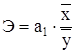. (12)

.

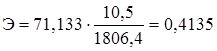Это значит, что при увеличении номера квартала на 1% величина прожиточного минимума возрастет на 0,41%.

4. Далее используем F-критерий Фишера, чтобы оценить статистическую надежность результатов регрессионного моделирования.

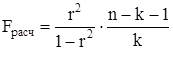. (13)

.

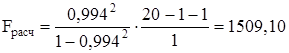Сравнивая полученное значение с табличным, видим, что F_расч > F_табл = 8,6718. Следовательно, в целом, модель значима.

Таким образом, модель признается адекватной и на ее основе можно принимать решения и осуществлять прогнозы.

5. Рассчитаем, чему должно быть равно прогнозное значение величины прожиточного минимума в 1 квартале 2005 года, во 2 квартале 2007 года, используя уравнение регрессии:

у_х = 1059,5 + 71,1 ∙ х.

1-ый квартал 2005 года имеет номер 21; 2-ый квартал 2007 года - 30.

Подставив эти значения в уравнения регрессии, получим:

- прогнозное значение для 1-го квартала 2005 года:

у_х = 1059,5 + 71,1 ∙ 21 = 2553,2 руб.;

- прогнозное значение для 2-го квартала 2007 года:

у_х = 1059,5 + 71,1 ∙ 30 = 3193,4 руб.

6. Определим доверительный интервал 2-ого прогноза для уровня значимости, равного 0,05.

Рассчитаем интегральную ошибку прогноза - Е_Y , которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии - S² _Y и ошибки прогноза положения регрессии - µ_Y . То есть:

.

В нашем случае

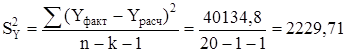
где k- число факторов в уравнении, которое в данной задаче равно 1.

Тогда = 47,22 руб.

Ошибка положения регрессии составит:

.

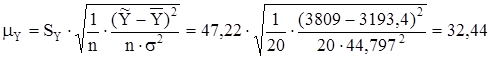32,44.