,

,

Тогда

Тогда

Ответ:

Задача 11

Исследовать на сходимость ряд:

а) с помощью признака Даламбера знакоположительный ряд

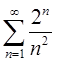
Решение

Проверим необходимый признак сходимости ряда

n®¥

n®¥

n®¥

?. ?. , ?? ??????????? ??????? ?????????? ???? ?? ???????????, ? ??? ??????????.

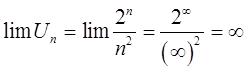
Используем признак Даламбера

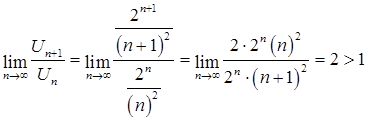
Ответ: ряд расходится

б) с помощью признака Лейбница знакочередующийся ряд

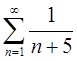
Решение

Проверим необходимый признак сходимости ряда

n®¥

n®¥

n®¥

?. ?. , ?? ??????????? ??????? ?????????? ???? ???????????, ????? ??????????? ??? ?? ??????????.

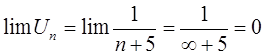
По признаку подобия

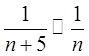
данный ряд аналогичен гармоническому ряду начиная с пятого члена, таким образом, т.к. гармонический ряд расходится, то и исходный ряд расходится.

Ответ: ряд расходится

в) Найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости

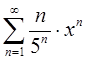
Решение

Используем признак Даламбера:

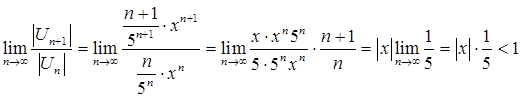
При х =5 получим ряд

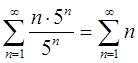
Ряд знакопостоянный, limUn = n

Ряд расходится, так как состоит из суммы возрастающих элементов, каждый из которых больше 1.

При х = -5 получим ряд