Контрольная работа: Решение матриц

Умножение

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы .

Это условие не выполняется, произведение АВ не существует.

Произведение матрицы и вектора А b :

Скалярное произведение векторов ( b ,с):

Найти определитель матрицы А:

В частности, формула вычисления определителя матрицы такова:

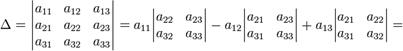
= a ₁₁ a ₂₂ a ₃₃ − a ₁₁ a ₂₃ a ₃₂ − a ₁₂ a ₂₁ a ₃₃ + a ₁₂ a ₂₃ a ₃₁ + a ₁₃ a ₂₁ a ₃₂ − a ₁₃ a ₂₂ a ₃₁

=2*(-4)*5 – 2*4*2 – (-2)*5*5 + (-2)*4*(-1) +(-1)*5*2 – (-1)*(-4)*(-1) = -40 – 16 +50 + 8 – 10 + 4 = -4

Найти обратную матрицу А^-1 :

Решение .

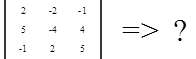
Определитель введенной Вами матрицы равен:

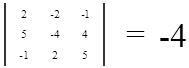
Определитель не равен нулю, следовательно обратная матрица существует.

Допишем к исходной матрице единичную матрицу справа.

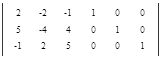
Начнем приведение левой квадратной матрицы к единичному виду. При помощи элементарных преобразований уберем все коэффициенты ниже главной диагонали.

Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.

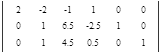
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.

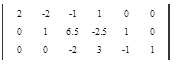
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.

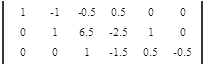
Приведем все коэффициенты выше главной диагонали к 0, при помощи элементарных преобразований.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--