Контрольная работа: Решение задач по теоретической механике

aт=dVt/dt = d[√(x'2 + y'2)] = (Vxax + Vyay)/V = 64t/[2√(1+16t2)]=32t/√(1+16t2)

При t=1 c aт=7,76 м/с2

Так как знаки скорости и касательного ускорения совпадают, точка движется ускоренно.

Нормальное ускорение:

an=√(a2 - a2т)

an = √(64-60,2176) = √3,7284 = 1,345 м/с2

Задача Д 8

Применение теоремы об изменении количества движения к исследованию движения механической системы.

Дано:

Найти: Скорость .

Решение:

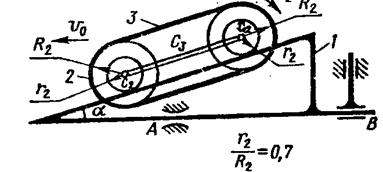
На механическую систему действуют внешние силы: - сила сухого трения в опоре А; - силы тяжести тел 1, 2 и 3; -сила нормальной реакции в точке А; -реактивный момент в опоре В.

Применим теорему об изменении количества движения механической системы в дифференциальной форме. В проекциях на оси координат

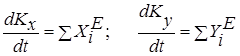, (1)

где - проекции вектора количества движения системы на оси координат; - суммы проекций внешних сил на соответствующие оси.

Количество движения системы тел 1, 2 и 3

(2)

где

. (3)

Здесь - скоростицентров масс тел 1, 2, 3; - соответственно переносные и относительные скорости центров масс.

Очевидно, что

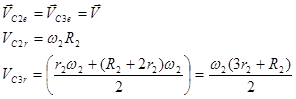(4)

Проецируя обе части векторного равенства (2) на координатные оси, получаем с учетом (3) и (4)

(5)

где - проекция вектора на ось;

Проекция главного вектора внешних сил на координатные оси