Контрольная работа: Сетевое планирование и управление Основы регрессионного анализа

Определим критический путь сетевого графика , т.е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю).

Рассмотрим все пути, проходящие через вершины сетевого графика с нулевыми резервами времени:

1) 1-5-6-7-8 . Его продолжительность равна:

(дней).

2) 1-5-8 . Его продолжительность равна:

(дней).

Таким образом, критическим путем является путь 1-5-6-7-8 и его продолжительность составляет 25 дней.

Перечень работ, принадлежащих критическому пути, представлен в таблице 1.2.

Таблица 1.2

Коды работ	Продолжительность работы (дни)
1-5	14
5-6	0
6-7	6
7-8	5

Найдём полный резерв времени работ.

Сетевой график выполнения работ по реконструкции цеха представлен на рисунке 1.3.

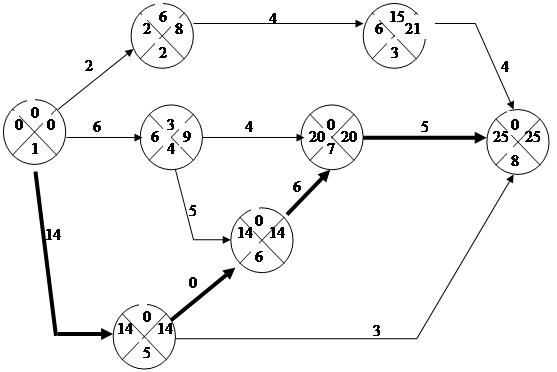
Рисунок 1.3

Ответ: Таким образом, критический путем является путь 1-5-6-7-8 и его длительность (продолжительность) составляет 25 дней.

2. Основы регрессионного анализа

2.1 Понятие корреляционного и регрессионного анализа

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).

Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.

Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена.

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от лат.correlatio соотношение, соответствие).

Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов. Характер связи между показателями определяется по корреляционному полю. Если у зависимый признак, а х независимый, то, отметив каждый случай х (i) с координатами и , получим корреляционное поле.

Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы.

Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от -0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.

Регрессионный анализсвоей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимо^; i или независимых переменных известна. Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются: а) на линейные: