Контрольная работа: Складність деяких методів експоненціювання точки кривої
Після розрахунку ![]() обчислюється точка
обчислюється точка ![]() методом ліворуч-праворуч за допомогою алгоритму 3.
методом ліворуч-праворуч за допомогою алгоритму 3.
Алгоритм 3.
Вхід:![]()
Вихід:![]()
1. ![]()
2. ![]()
2.1 ![]()
2.2 ![]()
2.3 ![]()
3. ![]() .
.
![]() -подання числа
-подання числа ![]() може виявитися на один біт більше двійкового. Водночас, для випадкового
може виявитися на один біт більше двійкового. Водночас, для випадкового ![]() ймовірність ненульових елементів
ймовірність ненульових елементів ![]() і
і ![]() знижується від
знижується від ![]() до
до ![]() , тобто, у середньому, для
, тобто, у середньому, для ![]() - розрядного числа їхня кількість оцінюється величиною
- розрядного числа їхня кількість оцінюється величиною ![]() . Тоді загальне середнє число групових операцій додавання
. Тоді загальне середнє число групових операцій додавання ![]() й подвоєння
й подвоєння ![]() в алгоритмі 3 можна оцінити як суму
в алгоритмі 3 можна оцінити як суму ![]()
Метод вікон з алгоритмом подвоєння - додавання - віднімання
Якщо в криптосистемі є резерви пам'яті, їх можна задіяти для подальшого збільшення швидкості обчислень. Ідея в тому, що замість точки ![]() можна експоненціювати і надалі складати суміжні блоки або вікна шириною
можна експоненціювати і надалі складати суміжні блоки або вікна шириною ![]() в
в ![]() - поданні точки
- поданні точки ![]()
Для цього розраховується за допомогою алгоритму 2 трійкове число ![]() , що потім може розбиватися на блоки довжиною, не менше
, що потім може розбиватися на блоки довжиною, не менше ![]()
Назвемо ![]() - вікном числа
- вікном числа 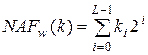 непарний коефіцієнт
непарний коефіцієнт ![]() утримуючий хоча б один ненульовий елемент. Зазначимо, що
утримуючий хоча б один ненульовий елемент. Зазначимо, що ![]()
![]() . Наприклад, при
. Наприклад, при ![]() маємо вісім різних значень
маємо вісім різних значень ![]()
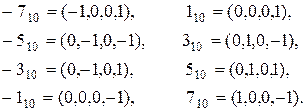
Цих вікон достатньо для формування числа ![]() довільної довжини
довільної довжини ![]() . Зазначимо, що парні коефіцієнти в
. Зазначимо, що парні коефіцієнти в ![]() - поданні числа
- поданні числа ![]() надлишкові, тому що вони утворяться подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються на згадку вісім точок:
надлишкові, тому що вони утворяться подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються на згадку вісім точок:![]() і
і ![]()
У загальному випадку в пам'яті зберігається ![]() точок. Число
точок. Число ![]() може бути визначене за допомогою модифікованого алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість
може бути визначене за допомогою модифікованого алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість ![]() необхідно записати
необхідно записати ![]() , де
, де ![]() означає ціле число
означає ціле число ![]() , певне в інтервалі
, певне в інтервалі ![]() . Далі обчислюється точка
. Далі обчислюється точка ![]() згідно з алгоритмом 4.
згідно з алгоритмом 4.
Алгоритм 4.
Вхід:![]()
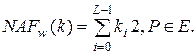
Вихід:![]()
1. ![]()
2. ![]()
3. ![]()
3.1 ![]()
3.2 ![]()
![]()
![]()
4. ![]() .
.
Нехай, наприклад,![]() при цьому
при цьому ![]() й
й ![]() Використання трійкового
Використання трійкового ![]() вимагає, мабуть, двох додавань точок, тоді як у другому випадку за рахунок попереднього розрахунку точки
вимагає, мабуть, двох додавань точок, тоді як у другому випадку за рахунок попереднього розрахунку точки ![]() достатньо одного додавання. Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна з'являється лише при порівняно більших довжинах
достатньо одного додавання. Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна з'являється лише при порівняно більших довжинах ![]() числа
числа ![]()