Контрольная работа: Статистика на предприятии
Коэффициент вариации меньше 33%, следовательно, совокупность является однородной, а средняя - типичной и устойчивой.
Задача 5
На основании аналитической группировки задачи 1 вычислить общую, межгрупповую и среднюю из внутригрупповых дисперсий. Определите корреляционное отношение по выработке одного рабочего. Сделайте выводы.
РЕШЕНИЕ:
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию и рассчитывается по формуле:
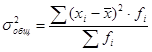
где - общая средняя по всей совокупности.
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
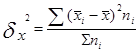
Где - средние по отдельным группам;
nj -численности по отдельным группам.
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
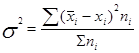
Средняя из внутригрупповых дисперсий:
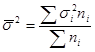
Закон, связывающий три вида дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
σ2 общ = δ2 + σ2
Данное соотношение называют правилом сложения дисперсий.
Для решения задачи сначала определим средние по каждой группе. Расчет средних выполнен в табл.5.
Средняя выработка в первой группе (до 3 лет) равна
х1 = 134,2 шт. (971: 5), во второй (от 3 до 10 лет) х2 = 127,0625 шт. (2033: 16), в третьей (свыше 10 лет) х3 = 142,667 шт. (1284: 9)
Промежуточные расчеты дисперсий по группам представлены в табл.5.
Таблица 5. - Расчет данных для определения внутригрупповых дисперсий.
|
№ рабочего |
Выработка (х) |
|
| ||
|
1 |
2 |
3 |
4 | ||
|
До 3 лет | |||||
|
К-во Просмотров: 701
Бесплатно скачать Контрольная работа: Статистика на предприятии
| |||||
