Контрольная работа: Теория информации. Статистический подход

Если студент учился плохо, можно заранее оценить возможные исходы сдачи экзамена, т.е. задать вероятности исходов, например, следующим образом: p (5) = 0.1; p (4) = 0.2; p (3) = 0.4; p (2) = 0.3.

В обоих случаях выполняется условие:

где n - число исходов опыта,

i - номер одного из исходов.

Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) - pi.

Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле:

I = - log2 pi,

где pi - вероятность i-го сообщения (исхода).

Пример 1. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для студента-хорошиста.

Пусть I (j) - количество информации в сообщении о получении оценки j. В соответствии с формулой Шеннона имеем:

I (5) = - log2 0,5 = 1,I (4) = - log2 0,3 = 1,74,I (3) = - log2 0,1 = 3,32

I (2) = - log2 0,1 = 3,32.

Пример 2. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для нерадивого студента:

I (5) = - log2 0,1 = 3,32,I (4) = - log2 0,2 = 2,32,I (3) = - log2 0,4 = 1,32,I (2) = - log2 0,3 = 1,74.

Таким образом, количество получаемой с сообщением информации тем больше, чем неожиданнее данное сообщение. Этот тезис использован при эффективном кодировании кодами переменной длины (т.е. имеющими разную геометрическую меру): исходные символы, имеющие большую частоту (или вероятность), имеют код меньшей длины, т.е. несут меньше информации в геометрической мере, и наоборот.

Формула Шеннона позволяет определять также размер двоичного эффективного кода, требуемого для представления того или иного сообщения, имеющего определенную вероятность появления.

Помимо информационной оценки одного сообщения, Шеннон предложил количественную информационную оценку всех сообщений, которые можно получить по результатам проведения некоторого опыта. Так, среднее количество информации Iср, получаемой со всеми n сообщениями, определяется по формуле:

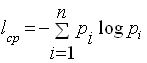
где pi - вероятность i-го сообщения.

Пример 3. Определить среднее количество информации, получаемое студентом-хорошистом, по всем результатам сдачи экзамена.

В соответствии с приведенной формулой имеем:

Iср = - (0,5*log20,5 + 0,3*log20,3 + 0,1*log20,1 + 0,1*log20,1) = 1,67.

Пример 4. Определить среднее количество информации, получаемое нерадивым студентом, по всем результатам сдачи экзамена.

В соответствии с приведенной формулой имеем:

Iср = - (0,1*log20,1 + 0,2*log20,2 + 0,4*log20,4 + 0,3*log20,3) = 1,73.

Большее количество информации, получаемое во втором случае, объясняется большей непредсказуемостью результатов: в самом деле, у хорошиста два исхода равновероятны.

Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. p1 = p2 = 0,5. Тогда имеем в соответствии с формулой для расчета I ср:

I ср = - (0,5*log20,5 + 0,5*log20,5) = 1.