Контрольная работа: Теорія споживання

Лінії цін характеризуються такими властивостями:

1) мають від’ємний нахил, який дорівнює зворотному співвідношенню цін двох товарів, тобто ;

2) при постійних цінах різним рівням доходу відповідають різні паралельні прямі; більшому доходу відповідає більш висока лінія цін.

При даних цінах і доході споживач прагне забезпечити максимум корисності. Цей максимум досягається в точці дотику самої верхньої кривої байдужності й лінії цін. Точка є точкою рівноваги, тобто у споживача немає будь-яких мотивів для перегляду даного плану покупок. Інша точка, що знаходиться на лінії цін, наприклад, точка , або нижча за неї, наприклад, точка , перебуватиме на більш низькій кривій байдужності, з більш низьким рівнем корисності та не влаштує споживача.

В точці рівноваги нахил лінії цін дорівнює нахилу кривої байдужності й забезпечує максимум корисності від закуповуваних товарів. При цьому виконується рівність відношення цін відношенню граничних корисностей товарів

, ,

,

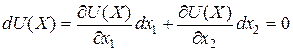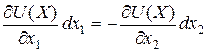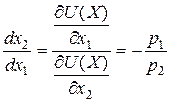де величина – гранична норма заміни двох благ.

Формально модель поведінки споживача на ринку є задачею нелінійного програмування з метою відшукання умовного максимуму

, (1)

або в розгорнутому вигляді

, , ,

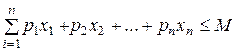де – вектор цін, – ціна -го товару, – витрати на -й товар. Отже, задача споживача полягає у виборі такого набору з множини , який є «найкращим», тобто для всіх інших наборів справедливе співвідношення .

Через те, що цільова функція безперервна, вона має додатні перші часткові похідні та вiд’ємно визначену матрицю Гессе, а також припустима множина замкнута й опукла, то відповідно до теореми Вейєрштраса розв’язок існує і єдиний.

Визначимо функцію Лагранжа

,

де –множник Лагранжа.

Необхідними й достатніми умовами для розв’язання задачі споживання (1.1) є умови Куна-Такера

, ,

,(2)

,

, , .

Вважають, що споживачі одержують усі види товарів і послуг. Тоді умова (2) матиме такий вигляд:

, , .(3)

Ці умови виконуються тільки в точці , де є оптимальним розв’язком (планом) задачі споживання.

Наприклад, у випадку двох товарів розв’язок має задовольняти системі

,

,

.