Контрольная работа: Теория вероятностей
Решение:
Пусть имеется множествоN элементов, из которых M элементов обладают некоторым признаком A . Извлекается случайным образом без возвращения n элементов. Вероятность события, что из m элементов обладают признаком А определяется по формуле:
(N=6, M=3, n=2, m=2)
Ответ:
Задание 5
Дана вероятность 
появления события A в каждом из 
независимых испытаний. Найти вероятность того, что в этих испытаниях событие A появится не менее 
и не более 
раз.
Решение:
Применим интегральную формулу Муавра-Лапласа
Где
и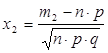 
Ф ( x) - функция Лапласа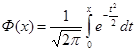 
, обладает свойствами
10 . 
- нечетная, т.е. 
20 . При 
, значения функции представлены таблицей (табулированы) для 
Так
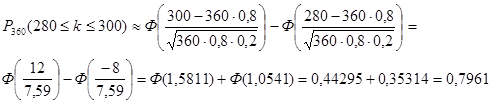
Ответ:
Задание 6
Задан закон распределения дискретной случайной величины X (в первой строке указаны возможные значения величины X, во второй строке даны вероятности p этих значение).
| Xi | 8 | 4 | 6 | 5 |
| pi | 0,1 | 0,3 | 0,2 | 0,4 |
Найти:
1) найти математическое ожидание 
,
2) дисперсию 
;
3) среднее квадратичное отклонение 
.
Математическое ожидание (ожидаемое среднее значение случайной величины):
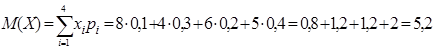
Дисперсия ( мера рассеяния значений случайной величины Х от среднего значения а ):
.
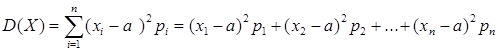